河北省承德市围场县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 下列四个选项中,与互为邻补角的是( )A、
 B、
B、 C、
C、 D、
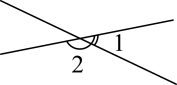
D、 2. 实数的值为( )A、 B、 C、 D、3. 如图是一把剪刀的示意图,我们可想象成一个相交线模型,若 , 则( )
2. 实数的值为( )A、 B、 C、 D、3. 如图是一把剪刀的示意图,我们可想象成一个相交线模型,若 , 则( ) A、 B、 C、 D、4. 下列不是二元一次方程组的是( )A、 B、 C、 D、5. 过点画线段所在直线的垂线段,其中正确的是( )A、
A、 B、 C、 D、4. 下列不是二元一次方程组的是( )A、 B、 C、 D、5. 过点画线段所在直线的垂线段,其中正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、7. 在平面直角坐标系中,如果点在第三象限,那么的取值范围是( )A、 B、 C、 D、8. 下列调查中,最适合采用普查方式的是( )A、市场监督管理局对当地粮食加工品质量安全的调查 B、年中央电视台春节联欢晚会收视率的调查 C、九年级某班学生每周参加体育锻炼时长的调查 D、全市初中学生参加家务劳动情况的调查9. 如图把三角板的直角顶点放在直线上,若 , , 则为( )
6. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、7. 在平面直角坐标系中,如果点在第三象限,那么的取值范围是( )A、 B、 C、 D、8. 下列调查中,最适合采用普查方式的是( )A、市场监督管理局对当地粮食加工品质量安全的调查 B、年中央电视台春节联欢晚会收视率的调查 C、九年级某班学生每周参加体育锻炼时长的调查 D、全市初中学生参加家务劳动情况的调查9. 如图把三角板的直角顶点放在直线上,若 , , 则为( )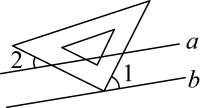 A、 B、 C、 D、10. 由方程组 可得出x与y的关系是( )A、x+y=1 B、x+y=﹣1 C、x+y=7 D、x+y=﹣711. 如图为嘉琪同学的答卷,她的得分应是( )分
A、 B、 C、 D、10. 由方程组 可得出x与y的关系是( )A、x+y=1 B、x+y=﹣1 C、x+y=7 D、x+y=﹣711. 如图为嘉琪同学的答卷,她的得分应是( )分姓名: 嘉琪 得分:____
填空(每小题20分,共100分)
①的倒数是 ________
②的绝对值是:________
③________
④平方根与立方根相等的数是 0和1
⑤________
A、 B、 C、 D、12. 小丽在用“加减消元法”解二元一次方程组时,利用消去 , 则、的值可能是( )A、 , B、 , C、 , D、 ,13. 为了响应国家“阳光体育”的号召,某校计划增设几项球类运动,学生会要统计本校学生最喜欢的球类运动,以下是排乱的调查统计步骤:①从扇形统计图中分析出最受学生欢迎的球类运动;②随机抽取200名学生,调查他们最喜欢的球类运动;③绘制扇形统计图;④整理所收集的数据.正确的调查统计步骤是( )A、②③①④ B、③④①② C、①②④③ D、②④③①14. 有一个不小于的两位数,个位上的数比十位上的数字小 , 则这个两位数是( )A、 B、 C、或 D、15. 为了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在次的学生人数占被调查学生人数的百分比为( ) A、 B、 C、 D、16. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为( ).A、 B、 C、 D、
A、 B、 C、 D、16. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为( ).A、 B、 C、 D、二、填空题
-
17. 如图所示,数轴上A,两点表示的数分别为和5.1,则A,两点之间表示整数的点共有个.
 18. 为了解某校七年级学生的阅读时间情况,对部分学生的阅读时间情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值),若该学校七年级共有200名学生,则阅读时间不低于3小时的是人.
18. 为了解某校七年级学生的阅读时间情况,对部分学生的阅读时间情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值),若该学校七年级共有200名学生,则阅读时间不低于3小时的是人.
 19. 如图, , , .
19. 如图, , , . (1)、;(2)、在直线上取一点 , 使得 , 则的度数是 .
(1)、;(2)、在直线上取一点 , 使得 , 则的度数是 .三、解答题
-
20.(1)、解方程组: .(2)、解不等式并将解集在数轴上表示出来: .(3)、如图, , , . 可推出 , 将下列证明过程空白处补充完整:
证明: , (已知)
(等量代换)
( )
(对顶角相等)
(等式的性质)
▲ ▲ ( )
21. 计算:(1)、(2)、(3)、22. 某汽车租赁公司要购买轿车和面包车共10辆,已知轿车每辆7万元,面包车每辆4万元,其中轿车至少要购买3辆,且公司可投入的购车款不超过55万元.(1)、符合公司要求的购买方案有几种?请说明理由.(2)、如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于1500元,那么该租赁公司应选择以上哪种购买方案?23. 每到春夏交替时节,杨絮漫天飞舞,给人们造成一定的困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.治理杨絮——您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
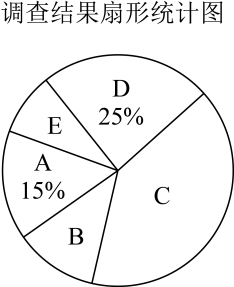

根据以上统计图,解答下列问题:
(1)、本次接受调查的市民共有人;(2)、扇形统计图中,扇形E的圆心角度数是°;(3)、请补全条形统计图;(4)、若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.24. 如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点. (1)、求△ABC的面积;(2)、如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.25. 宁波杨梅季,本地慈溪杨梅在宁波人的心中是一种家乡的味道.今年是杨梅大年,某杨梅种植大户为了能让居民品尝到物美价廉的杨梅,对1000斤的杨梅进行打包方式优惠出售,打包方式及售价如下:圆篮每篮8斤,售价160元;方篮每篮18斤,售价270元.假如用这两种打包方式恰好全部装完这1000斤杨梅.(1)、若销售a篮圆篮和a篮方篮共收入8600元,求a的值;(2)、当销售总收入为16760元时,
(1)、求△ABC的面积;(2)、如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.25. 宁波杨梅季,本地慈溪杨梅在宁波人的心中是一种家乡的味道.今年是杨梅大年,某杨梅种植大户为了能让居民品尝到物美价廉的杨梅,对1000斤的杨梅进行打包方式优惠出售,打包方式及售价如下:圆篮每篮8斤,售价160元;方篮每篮18斤,售价270元.假如用这两种打包方式恰好全部装完这1000斤杨梅.(1)、若销售a篮圆篮和a篮方篮共收入8600元,求a的值;(2)、当销售总收入为16760元时,①若这批杨梅全部售完,请问圆篮共包装了多少篮,方篮共包装了多少篮;
②若杨梅大户留下篮圆篮送人,其余的杨梅全部售出,求b的值.
26. 已知:如图, .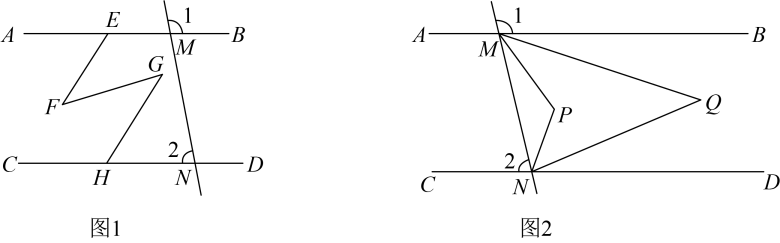 (1)、如图1, , 判断直线和的位置关系,并给予证明;(2)、如图2, , , 请判断与的数量关系,并证明.
(1)、如图1, , 判断直线和的位置关系,并给予证明;(2)、如图2, , , 请判断与的数量关系,并证明.