河北省张家口市宣化区2022-2023学年七年级下学期期末数学试题（冀教版）

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组中的三条线段（单位： $c m$ ），能围成三角形的是（）

A、1，2，3 B、2，3，4 C、10，20，35 D、4，4，9

查看试题解析
2. 根据如图信息可知，下列关于温度 $x (℃)$ 的不等式正确的是（）
洗涤说明
手洗，勿浸泡，不超过 $40 ℃$ 水温

A、 $x > 40$ B、 $x < 40$ C、 $x \leq 40$ D、 $x \geq 40$

查看试题解析
3. 不等式 $2 x - 1 < 4 (x + 1)$ 的解集表示在如图所示的数轴上，则阴影部分盖住的数是（）

A、 $- 1$ B、 $- 2$ C、 $- 1.5$ D、 $- 2.5$

查看试题解析
4. 下列等式从左边到右边的变形，属于因式分解的是（）

A、2ab（a-b）=2a²b-2ab² B、x²+1=x（x+ $\frac{1}{x}$ ） C、x²-4x+3=（x-2）²-1 D、a²-b²=（a+b）（a-b）

查看试题解析
5. 下列运算正确的是（）

A、 $3^{- 2} = 9$ B、 ${(- 2)}^{0} = 0$ C、 $2 a^{2} \cdot a^{3} = 2 a^{6}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
6. 下列多项式能用平方差公式分解因式的是（）

A、4x²+y² B、-4x²-y² C、-4x²+y² D、-4x+y²

查看试题解析
7. 如图， $∠ 1 + ∠ 2 + ∠ 3 = 232 °$ ， $A B ∥ D F$ ， $B C ∥ D E$ ，则 $∠ 3 - ∠ 1$ 的度数为（）

A、 $76 °$ B、 $52 °$ C、 $75 °$ D、 $60 °$

查看试题解析
8. 如图所示，AC⊥BC于C，CD⊥AB于D，图中可以作为三角形“高”的线段有（）

A、1条 B、2条 C、3条 D、5条

查看试题解析
9. 二元一次方程 $x + 3 y = 4$ 有一组解互为相反数，则y的值为（）

A、2 B、1 C、0 D、-1

查看试题解析
10. 如图是测量一颗玻璃球体积的过程：（1）将300ml的水倒进一个容量为500ml的杯子中；（2）将四颗相同的玻璃球放入水中，结果水没有满；（3）再加一颗同样的玻璃球放入水中，结果水满溢出．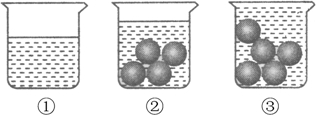
根据以上过程，推测这样一颗玻璃球的体积在（）

A、20cm³以上，30cm³以下 B、30cm³以上，40cm³以下 C、40cm³以上，50cm³以下 D、50cm³以上，60cm³以下

查看试题解析
11. 如图，D，E，F分别是边BC，AD，AC上的中点，若S阴影的面积为3，则△ABC的面积是（）

A、5 B、6 C、7 D、8

查看试题解析
12. 某商城开设一种摸奖游戏，中一等奖的机会为20万分之一，将这个数用科学记数法表示为（）

A、2×10^﹣⁵ B、2×10^﹣⁶ C、5×10^﹣⁵ D、5×10^﹣⁶

查看试题解析
13. 不论a为何实数，多项式 $a^{2} + 4 a + 5$ 的值一定是（）

A、正数 B、负数 C、零 D、不能确定

查看试题解析
14. 如图， $△ A B C$ 的角平分线 $C D$ ， $B E$ 相交于F， $∠ A = 90 °$ ， $E G ∥ B C$ ，且 $C G ⊥ E G$ 于G，下列结论：① $∠ C E G = 2 ∠ D C B$ ；② $C A$ 平分 $∠ B C G$ ；③ $∠ A D C = ∠ G C D$ ；④ $∠ D F B = \frac{1}{2} ∠ C G E$ ．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

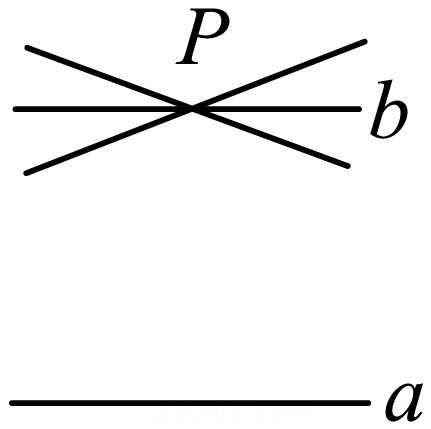
15. 如图，在直线a外有一点P，经过点P可以画无数条直线，如果 $a / / b$ ，那么过点P的其它直线与直线a一定不平行，理由是．

查看试题解析
16. 如图，将 $△ A B C$ 沿 $D E$ ， $H G$ ， $E F$ 翻折，三个顶点均落在点O处，若 $∠ 1 = 131 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
17. 若(a²－1)⁰＝1，则a的取值范围是．

查看试题解析
18. 已知二元一次方程组 ${\begin{array}{l} 3 x - 7 y = - 1 \\ 3 x + 7 y = 13 \end{array}$ 的解满足不等式 $a x + 2 y < 5$ ，则a的取值范围是．

查看试题解析
19. 已知x=4是不等式ax-3a-1<0的解，x=2不是不等式ax-3a-1<0的解，则实数a的取值范围是.

查看试题解析
20. 甲、乙两个同学分解因式x²+ax+b时，甲看错了b，分解结果为(x+2)(x+4)；乙看错了a，分解结果为(x+1)(x+9)，则a-b的值是．

查看试题解析

三、解答题

21. 计算：

(1)、解不等式： $\frac{2 x - 1}{5} - \frac{x - 2}{3} \geq 1$ ；

(2)、计算： $(2 x - 3 y) (- 2 x - 3 y)$ ；

(3)、利用因式分解计算： $201 8^{2} - 4036 \times 1018 + 101 8^{2}$

查看试题解析
22. 解不等式组： ${\begin{array}{l} 3 (x + 2) \geq 2 x + 5 \\ \frac{x}{3} - 1 < \frac{x - 2}{2} \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
23. 某社区购买甲、乙两种树苗进行绿化，已知甲种树苗每棵30元，乙种树苗每棵20元，且乙种树苗棵数比甲种树苗棵数的2倍少40棵，购买两种树苗的总金额为9000元．

(1)、求购买甲、乙两种树苗各多少棵？

(2)、为保证绿化效果，社区决定再购买甲、乙两种树苗共10棵（可以只买一种），总费用不超过230元，求可能的购买方案？

查看试题解析
24.

(1)、你能求出（a-1）（ $a^{99} + a^{98} + a^{97} + \cdot \cdot \cdot + a^{2}$ +a+1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．
（a-1）（a+1）＝；
（a-1）（ $a^{2}$ +a+1）＝；
（a-1）（ $a^{3} + a^{2}$ +a+1）＝；
由此我们可以得到：（a-1）（ $a^{99} + a^{98}$ +…+a+1）＝．

(2)、利用（1）的结论，完成下面的计算：
$2^{199} + 2^{198} + 2^{197} + \cdot \cdot \cdot + 2^{2}$ +2+1．

查看试题解析
25. 若一元一次方程的解也是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．
例如：方程 $2 x - 6 = 0$ 的解为 $x = 3$ ，不等式组 ${\begin{array}{l} x - 2 > 0 \\ x < 5 \end{array}$ 的解集为 $2 < x < 5$ ，因为 $2 < 3 < 5$ ，所以方程 $2 x - 6 = 0$ 为不等式组 ${\begin{array}{l} x - 2 > 0 \\ x < 5 \end{array}$ 的关联方程．

(1)、在方程① $5 x - 3 = 0$ ， ② $x - 3 = 0$ 中，不等式组 ${\begin{array}{l} 2 x - 5 \geq 3 x - 8 \\ 3 < 5 x \end{array}$ 的关联方程是（填序号）；

(2)、若不等式组 ${\begin{array}{l} x - \frac{1}{4} < 1 \\ 9 x \geq 1 \end{array}$ 的一个关联方程的解是整数，则这个关联方程的解是；

(3)、若方程 $x = 2$ 与 $x = 3$ 都是关于x的不等式组 ${\begin{array}{l} x > m \\ x - 2 \leq m \end{array}$ 的关联方程，求m的取值范围．

查看试题解析
26. 如图，直线AB∥CD，直线l与直线AB、CD相交于点E、F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处．

(1)、若∠PEF＝48°，点Q恰好落在其中的一条平行线上，求则∠EFP的度数；

(2)、若∠PEF＝75°，2∠CFQ＝∠PFC，求∠EFP的度数．

查看试题解析