山东省德州市乐陵市2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最小的数是（）

A、 $- \sqrt{2}$ B、0 C、1 D、 $\sqrt[3]{- 8}$

查看试题解析
2. 已知l₁∥l₂ ，一个含有30°角的三角尺按照如图所示位置摆放，则∠1+∠2的度数为（　　）

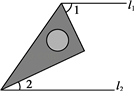A、90° B、120° C、150° D、180°

查看试题解析
3. 在平面直角坐标系中，将点 $(2 ， 1)$ 向下平移3个单位长度，所得点的坐标是（）

A、 $(2 ， 4)$ B、 $(2 ， - 2)$ C、 $(- 1 ， 1)$ D、 $(5 ， 1)$

查看试题解析
4. 下列各组数中，是二元一次方程5x-y=4的一个解的是（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 6 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
5. 已知实数a，b满足a+1＞b+1，则下列选项错误的为（）

A、a＞b B、a+2＞b+2 C、﹣a＜﹣b D、2a＞3b

查看试题解析

6. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、

\frac{x}{4} + \frac{y}{3} = \frac{42}{60}

B、

\frac{x}{5} + \frac{y}{4} = \frac{42}{60}

C、

\frac{x}{4} + \frac{y}{5} = \frac{42}{60}

D、

\frac{x}{3} + \frac{y}{4} = \frac{42}{60}

查看试题解析

7. 如图，《九章算术》现今流传的大多是在三国时期魏元帝景元四年( $263$ 年)，刘徽为《九章》所作的注本《九章算术》内容十分丰富，全书总结了战国、秦、汉时期的数学成就，是一本综合性的历史著作，是当时世界上最简练有效的应用数学，它的出现标志中国古代数学形成了完整的体系《九章算术》不仅最早提到分数问题，也首先记录了盈不足等问题，《九章算术》卷七“盈不足”有如下记载：“今有共买物，人出八，盈三；人出七，不足四问人数、物价各几何？”译文：“今有人合伙购物，每人出 $8$ 钱，会多 $3$ 钱；每人出 $7$ 钱，又差 $4$ 钱．问人数、物价各多少？”设合伙人数为 $x$ 人，物价为 $y$ 钱，以下列出的方程组正确的是（）

A、 ${\begin{array}{l} 8 x - y = 3 \\ y - 7 x = 4 \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ D、 ${\begin{array}{l} y - 8 x = 3 \\ 7 x - y = 4 \end{array}$

查看试题解析
8. 如图，已知每一个同类水果的质量相同， $a$ ， $b$ ， $c$ 分别表示一个苹果、一个梨、一个桃子的质量，则下列关系中正确的是（）

A、 $a > c > b$ B、 $b > a > c$ C、 $a > b > c$ D、 $c > a > b$

查看试题解析
9. 荆州古城是闻名遐迩的历史文化名城，“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查，整理后绘制了两幅统计图（尚不完整）．根据图中信息，下列结论错误的是（）

A、本次抽样调查的样本容量是5000 B、扇形图中的m为10% C、样本中选择公共交通出行的有2500人 D、若“五一”期间到荆州观光的游客有50万人，则选择自驾方式出行的有25万人

查看试题解析
10. 不等式组 ${\begin{array}{l} 2 x + 9 > 6 x + 1 \\ x - k < 1 \end{array}$ 的解集为 $x < 2$ ，则 $k$ 的取值范围为（）

A、 $k > 1$ B、 $k < 1$ C、 $k \geq 1$ D、 $k \leq 1$

查看试题解析
11.
周末，小明与小文相约一起到游乐园去游玩，如图是他俩在微信中的一段对话：
根据上面两人的对话纪录，小文能从M超市走到游乐园门口的路线是（　　）

A、向北直走700米，再向西直走300米 B、向北直走300米，再向西直走700米 C、向北直走500米，再向西直走200米 D、向南直走500米，再向西直走200米

查看试题解析
12. 规定：对于任意实数x，通常用[x]表示不超过x的最大整数，如：[π]=3，[2]=2，[-2.1]=-3给出下列结论：①[-x]=-x；②若[x]=n，则x的取值范围是n≤x<n+1；③当-1<x<1时，[1+x]+[1-x]的值为1或2；④x=-2.75是方程4x-2[x]+5=0的唯一解．其中正确结论的序号是（）

A、①② B、②③ C、①③ D、③④

查看试题解析

二、填空题

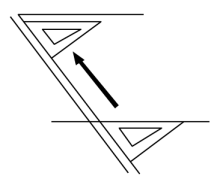
13. 16的算术平方根是

查看试题解析
14. 如图，给出了直线外一点作已知直线平行线的一种方法，它的依据是。

查看试题解析
15. 某雷达探测目标得到的结果如图所示，若记图中目标A的位置为（3，30°），目标B的位置为（2，180°），目标C的位置为（4，240°），则图中目标D的位置可记为．

查看试题解析
16. 若 $x ， y$ 满足方程组 ${\begin{array}{l} x + 4 y = 4 ， \\ 2 x - 2 y = 13 ， \end{array}$ 则 $3 x + 2 y$ 的值为．

查看试题解析
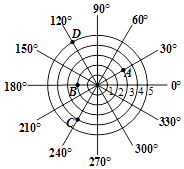17. 若关于 $x$ 、 $y$ 的二元一次方程组 ${\begin{array}{l} x - 3 y = 4 m + 3 \\ x + 5 y = 5 \end{array}$ 的解满足 $x + y \leq 0$ ，则 $m$ 的取值范围是.

查看试题解析
18. 如图，在平面直角坐标系中， $A (1 ， 1)$ ， $B (- 1 ， 1)$ ， $C (- 1 ， - 2)$ ， $D (1 ， - 2)$ ．把一条长为2023个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按 $A \to B \to C \to D \to A \to$ …的规律紧绕在四边形 $A B C D$ 的边上，则细线另一端所在位置的点的坐标是．

查看试题解析

三、解答题

19. 计算

(1)、计算： $\sqrt{25} - \sqrt[3]{27} - | \sqrt{3} - 2 |$

(2)、解方程： ${\begin{array}{l} x - y = 1 \\ 3 x + y = 7 \end{array}$

查看试题解析
20. 数学课上，陈老师说：“同学们，如果 $∠ A$ 的两边与 $∠ C$ 的两边分别平行，你能根据这个条件画出图形并探讨一下 $∠ A$ 与 $∠ C$ 的数量关系吗?”

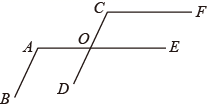(1)、甲同学很快画出了如图所示的图形，并根据 $A B // C D$ ， $A E // C F$ 的条件，得出了 $∠ A = ∠ C$ 的结论，请你帮他写出说理过程．

(2)、甲同学由此告诉陈老师：“我的结论是：如果两个角的两边分别平行，那么这两个角相等．”你同意甲同学的结论吗? ．（填“同意”或“不同意”）．如果不同意，请写出你的结论：．

查看试题解析
21. 今年3月5日，我校组织全体学生参加了“走出校门，服务社会”的活动．九年级三班同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图．请根据同学所作的两个图形．解答：

(1)、九年级三班有多少名学生；

(2)、补全直方图的空缺部分；

(3)、若九年级有800名学生，估计该年级去敬老院的人数．

查看试题解析
22. 已知 $x = 1 - 2 a ， y = 3 a - 4$ ．

(1)、已知x的算术平方根为3，求a的值；

(2)、如果x，y都是同一个数的平方根，求这个数．

查看试题解析
23. 为落实“绿水青山就是金山银山”的发展理念，某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务．该工程队有 $A ， B$ 两种型号的挖掘机，已知3台 $A$ 型和5台 $B$ 型挖掘机同时施工一小时挖土165立方米；4台 $A$ 型和7台 $B$ 型挖掘机同时施工一小时挖土225立方米．每台 $A$ 型挖掘机一小时的施工费用为300元，每台 $B$ 型挖掘机一小时的施工费用为180元．

(1)、分别求每台 $A$ 型， $B$ 型挖掘机一小时挖土多少立方米?

(2)、若不同数量的 $A$ 型和 $B$ 型挖掘机共12台同时施工4小时，至少完成1080立方米的挖土量，且总费用不超过12960元．问施工时有哪几种调配方案，并指出哪种调配方案的施工费用最低，最低费用是多少元?

查看试题解析
24. 综合与实践：

(1)、问题背景：
已知A（1，2），B（3，2），C（1，-1），D（-3，-3）．在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P₁、P₂ ，然后写出它们的坐标，则P₁ ▲ ， P₂ ▲ ．

(2)、探究发现：
结合上述计算结果，你能发现若线段的两个端点的坐标分别为（x₁ ， y₁），（x₂ ， y₂），则线段的中点坐标为．

(3)、拓展应用：
利用上述规律解决下列问题：已知三点E（-1，2），F（3，1），G（1，4），第四个点H（x，y）与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．

查看试题解析
25. 同学们，我们一起观察小猪的猪蹄，你会发现一个我们熟悉的几何图形，我们就把这个图形形象的称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．

(1)、如图①， $A B ∥ C D$ ， $E$ 为 $A B$ ， $C D$ 之间一点，连接 $B E$ ， $D E$ ，得到 $∠ B E D$ ．试探究 $∠ B E D$ 与 $∠ B$ 、 $∠ D$ 之间的数量关系，并说明理由．

(2)、请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：
①如图②， $A B ∥ C D$ ，线段 $A D$ 与线段 $B C$ 相交于点 $E$ ， $∠ B A D = 36 °$ ， $∠ B C D = 80 °$ ， $E F$ 平分 $∠ B E D$ 交直线 $A B$ 于点 $F$ ，求 $∠ B E F$ 的度数．

②如图③， $A B ∥ C D$ ，线段 $A D$ 与线段 $B C$ 相交于点 $E$ ， $∠ B A D = 36 °$ ， $∠ B C D = 80 °$ ，过点 $D$ 作 $D G ∥ C B$ 交直线 $A B$ 于点 $G$ ， $A H$ 平分 $∠ B A D$ ， $D H$ 平分 $∠ C D G$ ，直接写出 $∠ A H D$ 的度数．

查看试题解析