山东省龙口市(五四制)2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 要说明命题“若 , 则”是假命题,可以举的一个反例是( )A、 B、 C、 D、2. 若是关于x 、y的二元一次方程ax-2y=1的解,则a的值为( )A、3 B、5 C、-3 D、-53. 一个不透明的布袋中装有1个白球和2个红球,它们除颜色不同以外其他都相同,从布袋中任意摸出一个球是白球的概率为( )A、 B、 C、 D、14. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
 A、 B、 C、 D、5. 如图,直线 , 将含有的三角板的直角顶点C放在直线b上,若 , 则的度数是( )
A、 B、 C、 D、5. 如图,直线 , 将含有的三角板的直角顶点C放在直线b上,若 , 则的度数是( )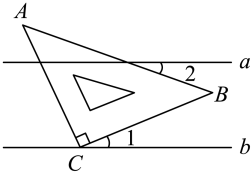 A、 B、 C、 D、6. 如图,直线经过点 , 则关于x的不等式解集为( )
A、 B、 C、 D、6. 如图,直线经过点 , 则关于x的不等式解集为( )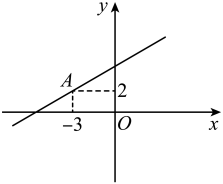 A、 B、 C、 D、7. 如图,中, , , 是斜边上的高, , 则的长是( )
A、 B、 C、 D、7. 如图,中, , , 是斜边上的高, , 则的长是( )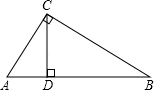 A、12 B、9 C、6 D、38. 甲、乙、丙、丁四个篮球队进行小组单循环比赛(每两队都要比赛一场),结果甲队胜了乙队,并且甲、丙、丁胜的场数相同,则这三队各胜的场数是( )A、0 B、1 C、2 D、39. 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分以的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A、12 B、9 C、6 D、38. 甲、乙、丙、丁四个篮球队进行小组单循环比赛(每两队都要比赛一场),结果甲队胜了乙队,并且甲、丙、丁胜的场数相同,则这三队各胜的场数是( )A、0 B、1 C、2 D、39. 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分以的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
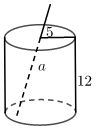 A、12≤a≤13 B、12≤a≤15 C、5≤a≤12 D、5≤a≤l310. 若关于x的不等式组无解,则a的取值范围为( )A、 B、 C、 D、
A、12≤a≤13 B、12≤a≤15 C、5≤a≤12 D、5≤a≤l310. 若关于x的不等式组无解,则a的取值范围为( )A、 B、 C、 D、二、填空题
-
11. 某个关于的不等式的解集在数轴上的表示如图所示,它的解集是 .
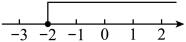 12. 如图, 的度数为 .
12. 如图, 的度数为 .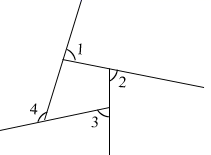 13. 如图,中,边的中垂线分别交于点的周长为 , 则的周长是 .
13. 如图,中,边的中垂线分别交于点的周长为 , 则的周长是 .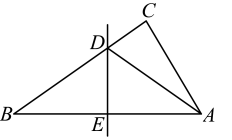 14. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为尺,那么索长尺.15. 如图所示的网格是由相同的小正方形组成的网格,点A,B,P是网格线的交点,则∠PAB+∠PBA= .
14. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为尺,那么索长尺.15. 如图所示的网格是由相同的小正方形组成的网格,点A,B,P是网格线的交点,则∠PAB+∠PBA= .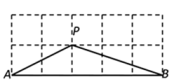 16. 某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100这100个数,抽到末位数字是5的可获得20元购物券,抽到数是66或99的可获得100元购物券,抽到数是88的可获得200元购物券.某顾客购物130元,他获得购物券的概率是 .
16. 某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100这100个数,抽到末位数字是5的可获得20元购物券,抽到数是66或99的可获得100元购物券,抽到数是88的可获得200元购物券.某顾客购物130元,他获得购物券的概率是 .三、解答题
-
17. 解方程组:18. 解不等式组:
要求:在解不等式组的过程中,在同一数轴上表示每个不等式的解集.
19. 如图,已知 , . 求证: . 20. 如图, , , E是上的一点,且 , . 求证: .
20. 如图, , , E是上的一点,且 , . 求证: .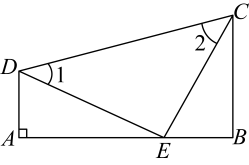 21. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
21. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:摸球的次数n
100
150
200
500
800
1000
…
摸到白球的次数m
58
96
116
295
484
601
…
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
…
(1)、请估计:当n很大时,摸到白球的频率将会接近;(2)、假如你去摸一次,你摸到白球的概率是 , 摸到黑球的概率是;(3)、试估算口袋中黑、白两种颜色的球各有多少只?22. 如图,在中, , 是上一点,的延长线与的延长线交于点 . 求证: .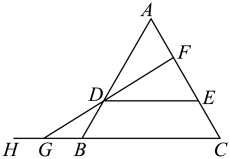 23. 已知:线段AB.
23. 已知:线段AB.
求作: , 使得 , .
作法:
①分别以点A和点B为圆心,AB长为半径作弧,两弧交于点D;
②连接BD,在BD的延长线上截取;
③连接AC.
则为所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接AD.
∵ ,
∴为等边三角形( ).(填推理的依据)
∴ .
∵ ,
∴ .
∴ ▲ ( ).(填推理的依据)
∴ .
∴ .
在中,
∴ .
24. 某中学组织师生共60人,从A市乘高铁前往B市参加学习交流活动,高铁票价格如表所示:(教师按成人票价购买,学生按学生票价购买)运行区间
一等座
二等座
出发站
终点站
成人票价(元/张)
成人票价(元/张)
学生票价(元/张)
A市高铁站
B市高铁站
132
80
60
若师生均购买二等座票,则共需3800元.
(1)、求参加活动的教师和学生各有多少人?(2)、由于部分教师需提早前往做准备工作,但合适的车次二等座已售完,这部分教师需购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有 人,购买一、二等座票全部费用为 元.①求 关于 的函数关系式;
②若购买一、二等座票全部费用不多于4000元,则提早前往的教师最多只能多少人?
25. 如图,已知 , A为y轴正半轴上一点,点D为第二象限一动点,点E在的延长线上,交于F,且 , 分别作于点M,于点N.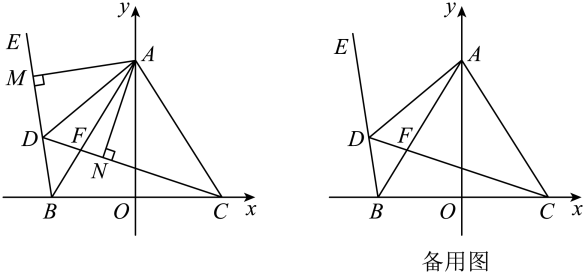 (1)、求证:;(2)、求证:平分;(3)、若点D在运动的过程中,始终有 , 请求出的度数.
(1)、求证:;(2)、求证:平分;(3)、若点D在运动的过程中,始终有 , 请求出的度数.