山东省济南市章丘区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 ${(a^{3})}^{2} = a^{6}$ B、 $2 a + 3 a = 5 a^{2}$ C、 $a^{8} \div a^{4} = a^{2}$ D、 $a^{2} \cdot a^{3} = a^{6}$

查看试题解析
2. 2022年9月9日，中国国家航天局、国家原子能机构联合宣布，我国研究团队首次在月球上发现新矿物，并命名为“嫦娥石”．“嫦娥石”也是人类发现的第六种月球新矿物，其单晶颗粒的粒径只有0.00000985米大小，数据0.00000985用科学记数法可表示为（）

A、 $9.85 \times$ $1 0^{6}$ B、 $98.5 \times$ $1 0^{- 7}$ C、 $9.85 \times$ $1 0^{- 6}$ D、 $9.85 \times$ $1 0^{- 5}$

查看试题解析
3. 小明在镜中看到对面电子时钟的示数如图所示，这现在的实际时间为（）

A、12：01 B、10： 21 C、15：10 D、10：51

查看试题解析
4. 小明家和小亮家到学校的直线距离分别是5km和3km，那么小明到小亮家的直线距离不可能是（）

A、1km B、2km C、3km D、8km

查看试题解析
5. 下列说法正确的是（）

A、天气预报说章丘区明天降水概率非常大，则明天章丘区会下雨是必然事件 B、某彩票中奖率为5%，小明买了4张这种彩票，前3张都没有中奖，则最后一张中奖的概率仍为5% C、任意抛掷一枚图钉10次，针尖全都向上，则抛掷一枚图钉针尖向上为必然事件 D、射击运动员射击一次只有2种可能的结果：中靶或脱靶，所以他中靶的概率为 $\frac{1}{2}$

查看试题解析
6. 如图，AC=DF，∠1=∠2，如果根据“ASA”判定△ABC≌△DEF，那么需要补充的条件是（）

A、∠A=∠D B、AB=DE C、BF=CE D、∠B=∠E

查看试题解析
7. 下列各式不能用平方差公式计算的是（）

A、 $(a + 2 b + c) (a - 2 b + c)$ B、 $(a - b - c) (- a + b + c)$ C、 $(a - b) (- a - b)$ D、 $(2 a + b) (b - 2 a)$

查看试题解析
8. 如图，将一纸条 $A B C D$ 沿折痕 $M G$ 折叠， $M A$ 对应线段 $M A^{'}$ 与 $C D$ 相交于点 $N$ 则下列条件中，不足以证明 $A B ∥ C D$ 的是（）

A、 $∠ B M N + ∠ C N M = 180 °$ B、 $∠ A M N = 2 ∠ M G N$ C、 $M N = N G$ D、 $M N = M G$

查看试题解析
9. 如图所示，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以 $B$ 为圆心，以任意长度为半径作弧，与 $B A$ ， $B C$ 分别交于点 $M$ 、 $N$ ，在分别以 $M$ 、 $N$ 为圆心，以大于 $\frac{1}{2}$ $M N$ 长度为半径作弧．两弧相交于点 $O$ ，作射线 $B O$ ．再分别以 $A$ 、 $B$ 为圆心，以大于 $\frac{1}{2}$ $A B$ 长度为半径作弧，两弧分别在线段 $A B$ 的上方和下方相交于点 $P$ 、 $Q$ ．直线 $P Q$ ．通过作图发现，射线 $B O$ 和直线 $P Q$ 恰好相交于边 $A C$ 上一点 $D$ ，则 $∠ A$ 的度数为 $($ )

A、 $20 °$ B、 $36 °$ C、 $30 °$ D、 $32 °$

查看试题解析
10. 甲乙两地相距 $300 k m$ ，一辆货车从甲地开往乙地，一辆轿车从乙地开往甲地，两车同时出发，中途不停留．各自到达目的地后停止，已知货车的速度为 $40 k m / h$ ．轿车的速度为 $60 k m / h$ ．设货车行驶时间为x（小时），两车间距离为y（千米），则下列图象中可以反映变量y与x之间关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. $(- 8)^{2023} \cdot (- \frac{1}{8})^{2022}$ $=$ ．

查看试题解析
12. 若 $(x + 2) (x + 5) = x^{2} + m x + n ，$ 则 $m + n =$ ．

查看试题解析
13. 将一副三角尺按照如图方式摆放，其中有一个角为 $30$ 的直角三角形的长直角边与等腰直角三角形的斜边平行，则 $∠ α$ 的度数为．

查看试题解析
14. “红灯停，绿灯行，黄灯亮了等一等”，某路口交通信号灯设计如下：每次红灯时间为30秒，绿灯时间为25秒，黄灯时间为5秒，如此循环往复，则某人驾车行驶至该路口，按照交通规则，需要停车等待的概率为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D E$ 是 $A C$ 的垂直平分线，分别交 $B C$ ， $A C$ 于点 $D$ ， $E$ ．若 $A C = 2$ ， $B C = 3$ ，则 $△ A B D$ 的周长是．

查看试题解析
16. 如图所示， $△ A B C$ 中， $A B = A C$ 且 $∠ B A C = 45 ° ， A D ， B E$ 分别为边 $B C 、 A C$ 边上的高， $A D ， B E$ 相交于点F，连接 $F C$ 则下列结论中：① $A D$ 垂直平分 $B C$ ；②图中有3个等腰三角形；③ $△ A E F ≌ △ B E C$ ；④ $A B$ 的长度恰与 $△ E F C$ 的周长相等；⑤如图，若点P是高 $A D$ 上一个动点，点Q是边 $A C$ 上一个动点，连接 $C P ， P Q$ ，则 $C P + P Q$ 的最小值等于 $B E$ 的长度，其中正确的是（只填序号）．

查看试题解析

三、解答题

17. 计算：

(1)、 $(3^{- 1} - 1)^{0} - 2^{- 2} + (- 3)^{2} - (\frac{1}{4})^{- 1}$

(2)、 $(6 m^{2} n - 6 m^{2} n^{2} - 3 m^{2}) \div (- 3 m^{2})$

查看试题解析
18. 先化简，再求值： $(a + 2 b) (a - 2 b) + (a - 2 b)^{2} - a (2 a + 3 b)$ ，其中 $a = \frac{1}{7} ， b = - 2023$ ．

查看试题解析
19. 已知：如图， $∠ 1 = ∠ C$ ， $∠ 2$ 和 $∠ D$ 互余， $B E ⊥ F D$ 于点 $G$ ，求证： $A B ∥ C D$ .

查看试题解析
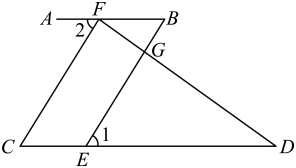20. 如图，在正方形网格中， $△ A B C$ 是格点三角形．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ，使得 $△ A_{1} B_{1} C_{1}$ 和 $△ A B C$ 关于直线 $l$ 对称；

(2)、请在直线 $l$ 上找一点 $P$ ，使点 $P$ 到 $A$ ， $C$ 两点的距离相等；

(3)、连接 $B A_{1}$ ， $B C_{1}$ ，求 $△ A_{1} B C_{1}$ 的面积．

查看试题解析
21. 一个不透明的口袋中装有6个红球，9个黄球，3个白球，这些球除颜色外其他均相同．从中任意摸出一个球．

(1)、求摸到的球是白球的概率；

(2)、小明又向这个口袋中放入了6个同样规格的球，若放入前后摸到白球的概率不变，则新放入的6个小球中有多少个白球?

查看试题解析
22. 如图所示，小安同学为电力公司设计了一个安全用电的标识，点 $A$ 、 $D$ 、 $C$ 、 $F$ 在同一条直线上，且 $A F = D C$ ， $B C = E F$ ， $B C ∥ E F$ ．

(1)、求证： $A B ∥ D E$ ；

(2)、若 $∠ A = 20 °$ ， $∠ A F E = 102 °$ ，求 $∠ E$ 的度数．

查看试题解析

23. 如图，当弹簧受到重力的作用时会伸长，某学习小组用实验的方式研究了一个弹簧的长度与所挂物体重量之间的关系，并对每组数据进行了记录：

物体的重量 $x / k g$	0	1	2	3	4	5	…
弹簧的长度 $y / c m$	9	11	13	15	17	19	…

(1)、上表所表示的变量之间的关系中，自变量是，因变量是．

(2)、当弹簧不悬挂重物时长度为cm，物体重量每增加

1 k g

，弹簧长度y增加cm；

(3)、直接写出y与x的关系式：．

(4)、当所挂物重为

6.5 k g

时，弹簧的长度为cm；

(5)、这根弹簧的弹性限度（即弹簧最长可以被拉长到的长度，超过这个长度，弹簧将失去弹性）为

25 c m

，则在弹性限度之内，该弹簧最多可以挂多重的物体?

查看试题解析

24. 在同一平面内，两条直线有平行和相交两种位置关系．

(1)、如图 $1$ 所示， $A B ∥ C D$ ，点 $E$ 为直线 $C D$ 下方的一点，连接 $B E$ 、 $D E$ ，线段 $B E$ 与直线 $C D$ 相交于点 $F$ ，试探究 $∠ B$ 、 $∠ D$ 、 $∠ E$ 之间的数量关系．
小明的解答过程如下 $：$
解： $∠ D + ∠ E = ∠ B$ ，理由如下：
      $∵$ $A B ∥ C D$ （已知） $∴$ $∠ B = ∠ B F D$ （）
又 $∵ ∠ B F D + ∠ D F E = 180 °$ $∴$ $∠ B + ∠ D F E$ $= 180 °$ （）即
      $∠ B =$       ▲            ；
      $∵$ 在 $△ D E F$ 中， $∠ D + ∠ E + ∠ D F E = 180 °$ （）
即 $∠ D + ∠ E = 180 - ∠ D F E$
      $∴$ $∠ D + ∠ E = ∠ B$ （等量代换）

(2)、如图 $2$ 所示， $A B ∥ C D$ ，当点 $E$ 移动到 $A B$ 、 $C D$ 之间时， $(1)$ 中结论是否仍成立，若成立，请说明理由；若不成立，请写出 $∠ B$ 、 $∠ D$ 、 $∠ B E D$ 之间的数量关系，并证明．
针对这个问题，小明、小亮、小颖三位同学各自提出了自己的解题思路：
小明：可以连接 $B D$ ，利用平行线的性质和三角形内角和和定理解决问题；
小亮：可以延长 $B E$ ，交 $C D$ 于点 $F$ ，同样利用平行线的性质和三角形内角和定理也可解决问题；
小颖：我过点 $E$ 做了一条与 $A B$ 平行的直线，也能做出来．
请从上述三种思路中选择一种，完成解答．

(3)、如图 $3$ 所示， $A B$ 与 $C D$ 相交干点 $F$ ，点 $E$ 为 $∠ B F D$ 内部一点，连接 $B E$ 、 $D E$ ，请直接写出 $∠ B$ 、 $∠ D$ 、 $∠ B E D$ 与 $∠ B F D$ 间的数量关系．

查看试题解析
25. 将完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 进行适当的变形，可以解决很多的数学问题．例如：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解：因为 $a + b = 3$ ，所以 ${(a + b)}^{2} = 9$ ，即 $a^{2} + 2 a b + b^{2} = 9$ ．
又因为 $a b = 1$ ，所以 $a^{2} + b^{2} = 7$ ．
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 8$ ， $x^{2} + y^{2} = 40$ ，则 $x y =$ ．

(2)、拓展：若 $(4 - x)^{2} + x^{2} = 10$ ，试求 $(4 - x) x$ 的值．

(3)、应用：如图，在长方形 $A B C D$ 中， $C D = 20 ， B C = 12$ ，点E、F是BC、CD上的点，且 $B E = D F = x$ ，分别以FC、CE为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，在长方形 $A B C D$ 内侧作长方形 $C E P F$ ，若长方形 $C E P F$ 的面积为160，求图中阴影部分的面积和．

查看试题解析
26.

(1)、如图1， $A B = A C ， ∠ B = ∠ E D F 、 D E = D F ， F C = 2 ， B E = 4$ ，求 $B C$ 的长度．

(2)、如图2， $A B = A C ， ∠ A B C = ∠ E D F ， D E = D F$ ，探索 $B C 、 B E 、 C F$ 的数量关系，并证明．

(3)、如图3，在 $△ A B C$ 中， $∠ B = ∠ A D E = 45 ° ， ∠ C = 22.5 ° ， D A = D E ， A B = b ， B D = a$ ，则 $D C =$ （用关于a、b的代数式表示）

查看试题解析