北师大版数学九年级上册同步练习—— 第四章 《图形的相似》7.相似三角形的性质
试卷更新日期:2023-07-26 类型:同步测试
一、选择题
-
1. 如果两个相似三角形的周长之比为1:2,那么这两个三角形的面积之比为( )A、1: B、1:2 C、1:4 D、1:82. 如图, , , , 则为( )
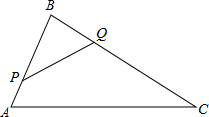
 A、8 B、 C、 D、103. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( )
A、8 B、 C、 D、103. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( ) A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S44. 若 , 且 , 若的周长为 , 则的周长为( )A、 B、 C、 D、5. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( )
A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S44. 若 , 且 , 若的周长为 , 则的周长为( )A、 B、 C、 D、5. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( ) A、1个 B、2个 C、3个 D、0个6. 如图, , , , 则的长为( )
A、1个 B、2个 C、3个 D、0个6. 如图, , , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,在中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;②以点D为圆心,以AM长为半径作弧,交DB于点;③以点为圆心,以MN长为半径作弧,在内部交前面的弧于点;④过点作射线交BC于点E. 若与四边形ACED的面积比为4:21,则的值为.
 8. 如图,中, , 点在上,且 , 点在上,连接 . 若 , 则 .
8. 如图,中, , 点在上,且 , 点在上,连接 . 若 , 则 . 9. 若△ABC∽△A′B′C′,且 , △ABC的周长为12cm,则△A′B′C′的周长为.10. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为.
9. 若△ABC∽△A′B′C′,且 , △ABC的周长为12cm,则△A′B′C′的周长为.10. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为. 11. 如图,点在等边三角形的边上,连接 , 线段的垂直平分线分别交边 , 于点 , 当时,的值为 .
11. 如图,点在等边三角形的边上,连接 , 线段的垂直平分线分别交边 , 于点 , 当时,的值为 . 12. 如图,已知四边形中,平分 , , , 如果与相似,那么 .
12. 如图,已知四边形中,平分 , , , 如果与相似,那么 .
三、解答题
-
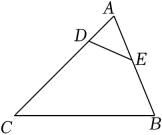
13. 如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.
 14. 如图,分别是、上的点, , , , , , 求的长和的度数.
14. 如图,分别是、上的点, , , , , , 求的长和的度数.