2023-2024学年北师大版数学七年级上册5.3 应用一元一次方程——水箱变高了(基础卷)
试卷更新日期:2023-07-26 类型:同步测试
一、选择题
-
1. 如图是一种正方形地砖的花型设计图,为了求这个正方形地砖的边长,可根据图示列方程( )
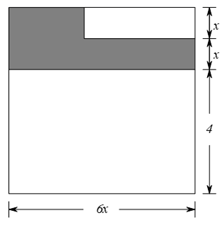 A、 B、 C、 D、2. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术其中,方程术是《九章算术》最高的数学成就.现有一个长方形的周长为 , 这个长方形的长减少 , 宽增加 , 就可以变成一个正方形,设长方形的宽为 , 可列方程为( )A、 B、 C、 D、3. 长方形的长是宽的3倍,如果宽增加了4m而长减少了5m,那么面积增加15m2 , 设长方形原来的宽为xm,所列方程是( )A、(x+4)(3x-5)+15= B、(x+4)(3x-5)-15= C、(x-4)(3x+5)-15= D、(x-4)((3x+5)+15=4. 将一个正方体钢坯锻造成长方体,它们的( )
A、 B、 C、 D、2. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术其中,方程术是《九章算术》最高的数学成就.现有一个长方形的周长为 , 这个长方形的长减少 , 宽增加 , 就可以变成一个正方形,设长方形的宽为 , 可列方程为( )A、 B、 C、 D、3. 长方形的长是宽的3倍,如果宽增加了4m而长减少了5m,那么面积增加15m2 , 设长方形原来的宽为xm,所列方程是( )A、(x+4)(3x-5)+15= B、(x+4)(3x-5)-15= C、(x-4)(3x+5)-15= D、(x-4)((3x+5)+15=4. 将一个正方体钢坯锻造成长方体,它们的( )
A、体积相等,表面积不相等 B、体积不相等,表面积相等 C、体积和表面积都相等 D、表面积相等,体积不相等5. 如图,大长方形是由5个完全相同的小长方形和一个边长为的正方形拼成,则大长方形的面积是( ) A、 B、 C、 D、6. 将边长为5的正方形分成若干个长方形,如果这若干个长方形恰好能拼成三个宽为1.5,长为a的长方形,则a的值为( )A、 B、 C、 D、7. 一张长为a,宽为b的长方形纸片(a>3b),分成两个正方形和一个长方形共三部分(如图所示),现将前两部分图形对折,折痕为AB,再将后两部分图形对折,折痕为CD,则长方形ABCD的周长为( )
A、 B、 C、 D、6. 将边长为5的正方形分成若干个长方形,如果这若干个长方形恰好能拼成三个宽为1.5,长为a的长方形,则a的值为( )A、 B、 C、 D、7. 一张长为a,宽为b的长方形纸片(a>3b),分成两个正方形和一个长方形共三部分(如图所示),现将前两部分图形对折,折痕为AB,再将后两部分图形对折,折痕为CD,则长方形ABCD的周长为( ) A、4b B、2(a-b) C、2a D、a+b8. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A、4b B、2(a-b) C、2a D、a+b8. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、56 B、40 C、28 D、209. 如图,小明将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为( )
A、56 B、40 C、28 D、209. 如图,小明将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为( )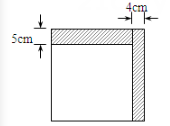 A、16 B、20 C、80 D、16010. 长方形ABCD可以分割成如图所示的七个正方形.若AB=10,则AD的长为( )
A、16 B、20 C、80 D、16010. 长方形ABCD可以分割成如图所示的七个正方形.若AB=10,则AD的长为( )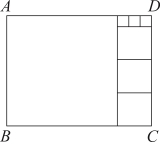 A、13 B、11 C、 D、11. 如图,A、O、B两点在数轴上对应的数分别为﹣20、0、40,C点在A、B之间,在A、B两点处各放一个挡板,M、N两个小球同时从C处出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变.设两个小球运动的时间为t秒钟(0<t<40),当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板.则:①C点在数轴上对应的数为0;②当10<t<25时,N在数轴上对应的数可以表示为80﹣4t;③当25<t<40时,2MA+NB始终为定值160;④只存在唯一的t值,使3MO=NO,以上结论正确的有( )
A、13 B、11 C、 D、11. 如图,A、O、B两点在数轴上对应的数分别为﹣20、0、40,C点在A、B之间,在A、B两点处各放一个挡板,M、N两个小球同时从C处出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变.设两个小球运动的时间为t秒钟(0<t<40),当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板.则:①C点在数轴上对应的数为0;②当10<t<25时,N在数轴上对应的数可以表示为80﹣4t;③当25<t<40时,2MA+NB始终为定值160;④只存在唯一的t值,使3MO=NO,以上结论正确的有( )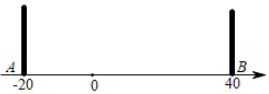 A、①②③④ B、①③ C、②③ D、①②④12. 在长方形 中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽 的长度为( ) cm .
A、①②③④ B、①③ C、②③ D、①②④12. 在长方形 中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽 的长度为( ) cm . A、1 B、1.6 C、2 D、2.513. 如图,啤酒瓶高为h,瓶内液体高为a,若将瓶盖好后倒置,液体高为a′(a′+b=h),则酒瓶的容积与瓶内酒的体积之比为( )
A、1 B、1.6 C、2 D、2.513. 如图,啤酒瓶高为h,瓶内液体高为a,若将瓶盖好后倒置,液体高为a′(a′+b=h),则酒瓶的容积与瓶内酒的体积之比为( )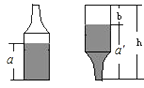 A、 B、 C、 D、14. 将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2 . 已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )
A、 B、 C、 D、14. 将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2 . 已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )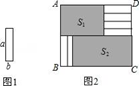 A、 b= a B、 b= C、 b=
A、 b= a B、 b= C、 b=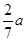 D、 b=
D、 b= 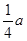 15. 如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( )
15. 如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( ) A、5 B、4 C、5或23 D、4或22
A、5 B、4 C、5或23 D、4或22二、填空题
-
16. 如图,在直线上顺次取 , , 三点,使得 , , 取线段的中点 , 若动点从点出发以的速度沿射线方向运动,设运动时间为 , 当时,的值为 .
 17. 已知长方形的长比宽大5,其周长为50,求其长、宽各是多少.设宽为x,列方程为 .
17. 已知长方形的长比宽大5,其周长为50,求其长、宽各是多少.设宽为x,列方程为 .
18. 将一个边长为10 cm正方形,沿粗黑实线剪下4个边长为 cm的小正方形,拼成一个大正方形,余下部分按虚线折叠成一个无盖长方体;最后把两部分拼在一起,组成一个完整的长方体,它的表面积等于原正方形的面积. 19. 老张在装修新房时想在客厅的地面按照图1所示的正方形图案铺贴仿古地板砖,图1是由四块尺寸完全相同的长方形砖拼成的一个正方形,中间还可另外嵌一个面积为的小正方形花砖(花砖老张已另买).但老张买砖时只看中了如图2所示的一款较大的正方形地砖,于是只能将其按照图3的方式切割出图1所需的长方形砖在进行铺贴,经过计算这样切割会让每块地砖产生废料.已知老张家客厅的面积为 , 请你帮老张算一下他需购买图2这款地砖块.
19. 老张在装修新房时想在客厅的地面按照图1所示的正方形图案铺贴仿古地板砖,图1是由四块尺寸完全相同的长方形砖拼成的一个正方形,中间还可另外嵌一个面积为的小正方形花砖(花砖老张已另买).但老张买砖时只看中了如图2所示的一款较大的正方形地砖,于是只能将其按照图3的方式切割出图1所需的长方形砖在进行铺贴,经过计算这样切割会让每块地砖产生废料.已知老张家客厅的面积为 , 请你帮老张算一下他需购买图2这款地砖块. 20. 如图,把一块长为的长方形硬纸板的四角剪去四个边长为的小正方形,然后把纸板沿虚线折起,做成一个无盖长方体纸盒.若纸盒的体积是 , 则长方形硬纸板的宽为 .
20. 如图,把一块长为的长方形硬纸板的四角剪去四个边长为的小正方形,然后把纸板沿虚线折起,做成一个无盖长方体纸盒.若纸盒的体积是 , 则长方形硬纸板的宽为 . 21. 如图,已知A,B两点在数轴上,点A表示的数为 , 点B表示的数为30,点M以每6个单位长度的速度从点A向右运动,点N以每秒2个单位长度的速度从点O向右运动,其中点M、点N同时出发,经过秒,点M、点N分别到点B的距离相等.
21. 如图,已知A,B两点在数轴上,点A表示的数为 , 点B表示的数为30,点M以每6个单位长度的速度从点A向右运动,点N以每秒2个单位长度的速度从点O向右运动,其中点M、点N同时出发,经过秒,点M、点N分别到点B的距离相等. 22. 如图,一个盛有水的长方体玻璃容器的内底面为边长为4cm的正方形,容器内水的高度为2cm,把一根长方体玻璃棒垂直放入容器中,其中玻璃棒底面为边长是2cm的正方形,则容器内的水将升高cm(假设水不会溢出).
22. 如图,一个盛有水的长方体玻璃容器的内底面为边长为4cm的正方形,容器内水的高度为2cm,把一根长方体玻璃棒垂直放入容器中,其中玻璃棒底面为边长是2cm的正方形,则容器内的水将升高cm(假设水不会溢出). 23. 如图,宽为50 cm的长方形图案是由10个相同的小长方形拼成的,其中一个小长方形的面积为cm2 .
23. 如图,宽为50 cm的长方形图案是由10个相同的小长方形拼成的,其中一个小长方形的面积为cm2 .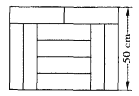
三、解答题
-
24. 一个正方形花圃边长增加2cm,所得新正方形花圃的周长是28cm,则:原正方形花圃的边长是多少?
25. 一根长米的铁丝围成一个长是宽的倍的长方形,求这个长方形的宽.26. 如图,用直径为200mm的钢柱锻造成一块长、宽、高分别为350mm,314mm,180mm的长方体坯底板.问应截取钢柱多长?(不计耗损,π取3.14)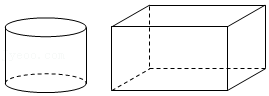 27. 如图1是边长为6的正方形硬纸版,在每个角上都剪去一个边长相等的小正方形,将其做成如图2的底面周长为16的正方形无盖纸盒,则这个无盖纸盒的高等于多少?
27. 如图1是边长为6的正方形硬纸版,在每个角上都剪去一个边长相等的小正方形,将其做成如图2的底面周长为16的正方形无盖纸盒,则这个无盖纸盒的高等于多少?
 28. 已知一个角的余角是这个角的补角的 ,求这个角的度数.29. 小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下类问题:
28. 已知一个角的余角是这个角的补角的 ,求这个角的度数.29. 小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下类问题: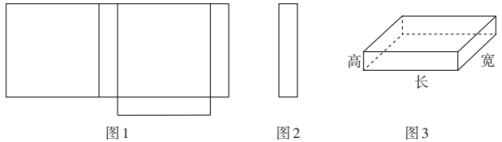
观察判断:
小明共剪开了 ▲ 条棱;
动手操作:
现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形:
解决问题:
经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是 , 求这个纸盒的体积.
30.实验室里,水平桌面上甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示,若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升cm,求开始注入多少分钟的水量后,甲与乙的水位高度之差是0.5cm?
