北师大版数学九年级上册同步练习—— 第四章 《图形的相似》6.利用相似三角形测高
试卷更新日期:2023-07-26 类型:同步测试
一、选择题
-
1. 常言道:失之毫厘,谬以千里.当人们向太空发射火箭或者描述星际位置时,需要非常准确的数据.的角真的很小.把整个圆等分成360份,每份这样的弧所对的圆心角的度数是 . . 若一个等腰三角形的腰长为1千米,底边长为4.848毫米,则其顶角的度数就是 . 太阳到地球的平均距离大约为千米.若以太阳到地球的平均距离为腰长,则顶角为的等腰三角形底边长为( )A、24.24千米 B、72.72千米 C、242.4千米 D、727.2千米2. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )
 A、3 B、4 C、5 D、63. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度的地方即同时使 , , 然后张开两脚,使、两个尖端分别在线段的两个端点上,若 , 则的长是( )
A、3 B、4 C、5 D、63. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度的地方即同时使 , , 然后张开两脚,使、两个尖端分别在线段的两个端点上,若 , 则的长是( ) A、 B、 C、 D、4. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( )
A、 B、 C、 D、4. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( ) A、 B、6 C、 D、85. 数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦的高度,如图,点处放一水平的平面镜.光线从点出发经平面镜反射后刚好射到大厦的顶端处,已知 , , 且测得米,米,米,那么该大厦的高度约为( )
A、 B、6 C、 D、85. 数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦的高度,如图,点处放一水平的平面镜.光线从点出发经平面镜反射后刚好射到大厦的顶端处,已知 , , 且测得米,米,米,那么该大厦的高度约为( )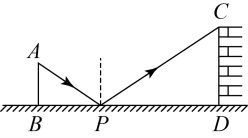 A、米 B、米 C、米 D、米6. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( )
A、米 B、米 C、米 D、米6. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( ) A、 B、 C、 D、7. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( )
A、 B、 C、 D、7. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( ) A、1cm B、cm C、2cm D、cm
A、1cm B、cm C、2cm D、cm二、填空题
-
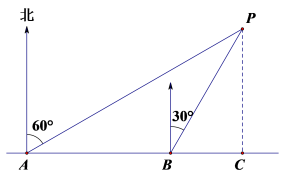
8. 小明同学在东西方向的环海路A处,测得海中灯塔在北偏东方向上,在处东600米的处,测得海中灯塔在北偏东30°方向上,则灯塔到环海路的距离米(用根号表示).
 9. 为测量校园水平地面上一棵树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把这面镜子水平放置在地面点E处,然后观测者沿着直线后退到点D,恰好在镜子里看到树的最高点A,再用皮尺测量 , 和观测者目高 . 若 , , , 则树的高度为m.
9. 为测量校园水平地面上一棵树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把这面镜子水平放置在地面点E处,然后观测者沿着直线后退到点D,恰好在镜子里看到树的最高点A,再用皮尺测量 , 和观测者目高 . 若 , , , 则树的高度为m. 10. 如图,利用标杆测量楼高,点A,D,B在同一直线上, , , 垂足分别为E,C.若测得 , , , 则楼高m.
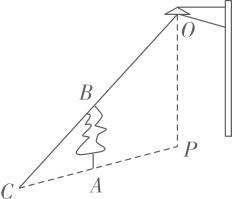
10. 如图,利用标杆测量楼高,点A,D,B在同一直线上, , , 垂足分别为E,C.若测得 , , , 则楼高m.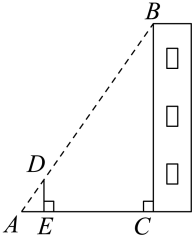 11. 图1是一种可调节桌面画架,画架侧面及相关数据如图2所示是底座OA上一固定支点,点C在滑槽DE内滑动,支杆BC长度不变.已知 , 当C从点D出发滑向终点E,从逐渐增大至 , 则支杆BC的长为 cm,若点F到OA的距离为40cm,则
11. 图1是一种可调节桌面画架,画架侧面及相关数据如图2所示是底座OA上一固定支点,点C在滑槽DE内滑动,支杆BC长度不变.已知 , 当C从点D出发滑向终点E,从逐渐增大至 , 则支杆BC的长为 cm,若点F到OA的距离为40cm,则 12. 如图,在平行四边形中,E为的中点,已知的面积为4,则的面积为 .
12. 如图,在平行四边形中,E为的中点,已知的面积为4,则的面积为 .
三、解答题
-
13. 西安钟楼位于西安市中心,明城墙内东西南北四条大街的交汇处,为中国现存钟楼中形制最大、保存最完整的一座.如图,小琪想要测出钟楼的高度,于是在地面上的C处放置了一面镜子,当他站在离镜子C处的E处时,恰好从镜子里看到钟楼顶端A在镜子中的像(即).已知B,C,E在同一直线上,小琪的眼睛离地面的高度 , , 求钟楼的高度.
 14. 位于陕西省渭南市澄城县城以南6公里处的印象古徵民俗文化园将现代都市生活与田园乡村气息完美结合,原汁原味的关中民俗风情诱惑着一批又一批的人前来游览.某个天气晴好的周末,欢欢和乐乐两个人去印象古徵民俗文化园游玩,看见园中的一棵大树,于是他们想运用所学知识测量这棵树的高度.如图,乐乐站在大树的影子的末端C处,同一时刻,欢欢在乐乐的影子的末端E处做上标记,随后两人用尺子测得米,米.已知乐乐的身高米,B、C、E在一条直线上, , . 请你运用所学知识,帮助欢欢和乐乐求出这棵大树的高度 .
14. 位于陕西省渭南市澄城县城以南6公里处的印象古徵民俗文化园将现代都市生活与田园乡村气息完美结合,原汁原味的关中民俗风情诱惑着一批又一批的人前来游览.某个天气晴好的周末,欢欢和乐乐两个人去印象古徵民俗文化园游玩,看见园中的一棵大树,于是他们想运用所学知识测量这棵树的高度.如图,乐乐站在大树的影子的末端C处,同一时刻,欢欢在乐乐的影子的末端E处做上标记,随后两人用尺子测得米,米.已知乐乐的身高米,B、C、E在一条直线上, , . 请你运用所学知识,帮助欢欢和乐乐求出这棵大树的高度 .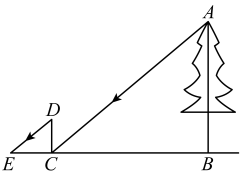 15. 如图,小树在路灯O的照射下形成投影.若树高 , 树影 , 树与路灯的水平距离 , 求路灯的高度.
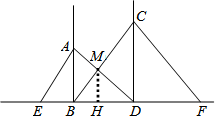
15. 如图,小树在路灯O的照射下形成投影.若树高 , 树影 , 树与路灯的水平距离 , 求路灯的高度. 16. 《海岛算经》是中国最早的一部测量数学专著,也是中国古代高度发达的地图学的数学基础.某班数学兴趣小组利用《海岛算经》中第一个问题的方法进行如下测量:如图,要测量一栋建筑物的高度 , 立两根高3米的标杆和 , 两杆之间的距离米,D,B,H成一线,从B处退5米到F,人的眼睛贴着地面观察A点,A,C,F三点成一线;从D处退6米到G,从G观察A点,A,E,G三点也成一线.请你帮助小组同学,试计算该建筑物的高度及的长.
16. 《海岛算经》是中国最早的一部测量数学专著,也是中国古代高度发达的地图学的数学基础.某班数学兴趣小组利用《海岛算经》中第一个问题的方法进行如下测量:如图,要测量一栋建筑物的高度 , 立两根高3米的标杆和 , 两杆之间的距离米,D,B,H成一线,从B处退5米到F,人的眼睛贴着地面观察A点,A,C,F三点成一线;从D处退6米到G,从G观察A点,A,E,G三点也成一线.请你帮助小组同学,试计算该建筑物的高度及的长.