北师大版数学九年级上册同步练习—— 第四章《图形的相似》4.探索三角形相似的条件（4）

试卷更新日期：2023-07-26 类型：同步测试

进入出卷网下载

一、选择题

1. 若点Р是线段 $A B$ 的黄金分割点 $(A P > P B)$ ， $A B = 2$ ，则 $A P$ 的长为（）

A、 $\sqrt{5} - 1$ B、 $3 - \sqrt{5}$ C、 $\sqrt{5} + 1$ D、 $3 + \sqrt{5}$

查看试题解析
2. 在学习画线段 $A B$ 的黄金分割点时，小明过点B作 $A B$ 的垂线 $B C$ ，取 $A B$ 的中点M，以点B为圆心， $B M$ 为半径画弧交射线 $B C$ 于点D，连接 $A D$ ，再以点D为圆心， $D B$ 为半径画弧，前后所画的两弧分别与 $A D$ 交于E，F两点，最后，以A为圆心，“■■”的长度为半径画弧交 $A B$ 于点H，点H即为 $A B$ 的其中一个黄金分割点，这里的“■■”指的是线段（）

A、 $A F$ B、 $D F$ C、 $A E$ D、 $D E$

查看试题解析
3. 若点C是线段AB的黄金分割点， $A C > B C ， A B = 8$ ，则AC的长度为（）

A、 $12 - 4 \sqrt{5}$ B、 $4 \sqrt{5} - 4$ C、5 D、 $2 \sqrt{5}$

查看试题解析
4. 校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄、金分割点(AP>PB)，如果AB的长度为10cm，那么AP的长度为（）cm．

A、 $\sqrt{5}$ -1 B、2 $\sqrt{5}$ -2 C、5 $\sqrt{5}$ -5 D、10 $\sqrt{5}$ -10

查看试题解析
5. 一般认为，如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割，则这个人身材好．如图，是一个参加空姐选拔的选手的实际身高情况，如果要使身材好，那么她穿鞋子的高度最好为（） $c m$ ．（精确到 $1 c m$ ，参考数据：黄金分割比为 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ）

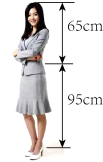A、5 B、8 C、10 D、12

查看试题解析
6. 点P是线段 $A B$ 的黄金分割点，且 $A P > P B$ ，则下列等式不成立的是（）

A、 $\frac{P B}{A P} = \frac{\sqrt{5} - 1}{2}$ B、 $\frac{A P}{A B} = \frac{\sqrt{5} - 1}{2}$ C、 $A P^{2} = A B \cdot B P$ D、 $A B^{2} = A P^{2} + P B^{2}$

查看试题解析

二、填空题

7. 如图，点 $B$ 为 $A C$ 上的黄金分割点 $(A B > B C)$ ， $B C = 2$ ，作如下操作：
步骤1：以点 $B$ 为圆心，小于1为半径作圆弧，分别与 $A B$ ， $B C$ 交于点 $M$ ， $N$ ；

步骤2：作 $M N$ 的中垂线 $B D$ ；

步骤3：以点 $B$ 为圆心， $B C$ 为半径为圆弧交 $B D$ 于点 $E$ ，连接 $A E$ .

则线段 $A E$ ， $A C$ ，圆弧 $C E$ 围成的几何图形面积为.

查看试题解析
8. 如图，在“黄金三角形” $A B C$ 中， $∠ A = 36 °$ ， $A B = A C$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，若 $C D = 1$ ，则 $A C$ 的长为．

查看试题解析
9. 黄金分割总能给人以美的享受，从人体审美学的角度看，若一个人上半身长与下半身长之比满足黄金比的话，则此人符合和谐完美的身体比例．一芭蕾舞演员的身高为160cm，但其上半身长与下半身长之比大于黄金比，当其表演时掂起脚尖，身高就可以增加10cm，这时上半身长与下半身长之比就恰好满足黄金比，那么该演员的上半身长为cm．（结果保留根号）

查看试题解析
10. 黄金分割在生活中的应用十分广泛，例如大多数窗户的宽和长的比是黄金比，已知某扇窗户的长为1.8米，则宽约为米．（结果精确到0.1）

查看试题解析
11. 宽与长的比等于黄金比的矩形称为黄金矩形．古希腊很多矩形建筑中宽与长的比都等于黄金比，如图，矩形ABCD为黄金矩形，AB＜AD，以AB为边在矩形ABCD内部作正方形ABEF，若AD＝1，则DF＝．

查看试题解析

三、解答题

12. 如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即 $A D = \frac{\sqrt{5} - 1}{2} A E$ ，BE交DC于点F，已知 $A B = \sqrt{5} + 1$ ，求CF的长 .

查看试题解析
13. 如图，点C 把线段 AB 分成两条线段 AC 和 BC，如果满足 $\frac{A C}{A B} = \frac{B C}{A C}$ ，那么我们称点C是线段 AB的黄金分割点，若AB=1，求AC的长．

查看试题解析
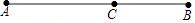
14.
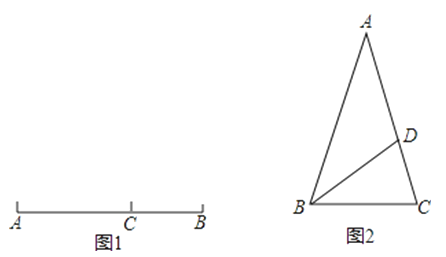
定义：如图1，点C在线段AB上，若满足AC²=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．

查看试题解析
15.
如图，△ABC中，AB=AC，∠A=36°，BD平分∠ABC．求证： $\frac{B C}{A B}$ = $\frac{\sqrt{5} - 1}{2}$ ．

查看试题解析

北师大版数学九年级上册同步练习—— 第四章 《图形的相似》4.探索三角形相似的条件（4）

一、选择题

二、填空题

三、解答题

北师大版数学九年级上册同步练习—— 第四章《图形的相似》4.探索三角形相似的条件（4）