广东省肇庆市德庆县2022-2023学年八年级(下)期末数学试卷
试卷更新日期:2023-07-25 类型:期末考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 要使有意义,则的值可以是( )A、 B、 C、 D、2. 如图,某公园的一块草坪旁边有一条直角小路,公园管理处为了方便群众,沿修了一条近路,已知米,米,则走这条近路要走米路.( )
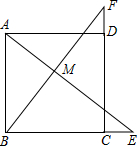
 A、 B、 C、 D、3. 不在函数图象上的点是( )A、 B、 C、 D、4. 下列各组线段中,能构成直角三角形的是( )A、2,3,4 B、3,4,6 C、5,6,8 D、5,12,135. 清溪中学在劳动基地开展主题为“春种秋收”的劳动教育活动,九年级班师生共参与了剪枝、锄地、除草、浇水、施肥五项实践活动,已知五个项目的参与人数分别是 , , , , , 则这组数据的众数和中位数分别是( )A、 , B、 , C、 , D、 ,6. 如图,矩形中,对角线、交于点若 , , 则的长为( )
A、 B、 C、 D、3. 不在函数图象上的点是( )A、 B、 C、 D、4. 下列各组线段中,能构成直角三角形的是( )A、2,3,4 B、3,4,6 C、5,6,8 D、5,12,135. 清溪中学在劳动基地开展主题为“春种秋收”的劳动教育活动,九年级班师生共参与了剪枝、锄地、除草、浇水、施肥五项实践活动,已知五个项目的参与人数分别是 , , , , , 则这组数据的众数和中位数分别是( )A、 , B、 , C、 , D、 ,6. 如图,矩形中,对角线、交于点若 , , 则的长为( ) A、 B、 C、 D、7. 若一次函数的图象平移后经过原点,下列平移方式正确的是( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位8. 如图,在一次实践活动课上,小明为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 , 然后取线段 , 的中点 , , 测量出 , 于是可以计算出池塘 , 两点间的距离是( )
A、 B、 C、 D、7. 若一次函数的图象平移后经过原点,下列平移方式正确的是( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位8. 如图,在一次实践活动课上,小明为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 , 然后取线段 , 的中点 , , 测量出 , 于是可以计算出池塘 , 两点间的距离是( )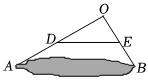 A、 B、 C、 D、9. 菱形具有而平行四边形不一定具有的性质是( )A、对角相等 B、对边相等 C、邻边相等 D、对边平行10. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( )
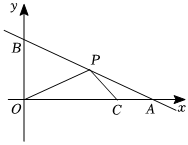
A、 B、 C、 D、9. 菱形具有而平行四边形不一定具有的性质是( )A、对角相等 B、对边相等 C、邻边相等 D、对边平行10. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
11. 计算: = .12. 如图,一棵高为的大树被台风刮断,若树在离地面处折断,树顶端刚好落在地可上,此处离树底部 处.
 13. 直线与x轴交点坐标为 .14. 甲、乙两名学生参加学校举办的“安全知识大赛”两人次成绩的平均数都是分,方差分别是 , , 则两人成绩比较稳定的是 填“甲”或“乙”15. 如图,在矩形中,对角线、的交点为 , 矩形的长、宽分别为、 , 过点分别交、于、 , 那么图中阴影部分面积为 .
13. 直线与x轴交点坐标为 .14. 甲、乙两名学生参加学校举办的“安全知识大赛”两人次成绩的平均数都是分,方差分别是 , , 则两人成绩比较稳定的是 填“甲”或“乙”15. 如图,在矩形中,对角线、的交点为 , 矩形的长、宽分别为、 , 过点分别交、于、 , 那么图中阴影部分面积为 .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
-
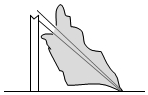
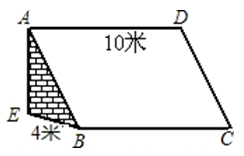
16. 计算: .17. 如图,小明准备建一个鲜花大棚,棚宽米,高米,长米,棚的斜面用矩形玻璃遮盖,不计墙的厚度,请计算阳光透过的最大面积.
 18. 已知一次函数的图象经过和两点.(1)、求这个一次函数的解析式;(2)、当时,求的值.19. 某些商家为消费者提供免费塑料袋使购物消费更加方便快捷,但是我们更应关注它对环境的潜在危害为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:
18. 已知一次函数的图象经过和两点.(1)、求这个一次函数的解析式;(2)、当时,求的值.19. 某些商家为消费者提供免费塑料袋使购物消费更加方便快捷,但是我们更应关注它对环境的潜在危害为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:每户丢弃塑料袋个数个
1
2
3
4
5
6
家庭数户
15
60
65
35
20
5
(1)、求当日这户家庭平均每户丢弃塑料袋的个数;(2)、假设我市现有家庭万户,据此估计全市所有家庭每年以天计算丢弃塑料袋的总数.20. 如图,在笔直的公路旁有一座山,从山另一边的处到公路上的停靠站的距离为 , 与公路上另一停靠站的距离为 , 停靠站、之间的距离为 , 为方便运输货物现要从公路上的处开凿隧道修通一条公路到处,且 . (1)、请判断的形状?(2)、求修建的公路的长.
(1)、请判断的形状?(2)、求修建的公路的长.