福建省福州市闽侯县2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-07-25 类型：期末考试

进入出卷网下载

1. 若二次根式 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq 2$ B、 $x \leq 2$ C、 $x \neq 2$ D、 $x \geq - 2$

查看试题解析
2. 下列给出的四组数中，能构成直角三角形三边的一组是（）

A、1，2，4 B、3，4，5 C、6，7，8 D、 $\sqrt{3}$ ， 3，6

查看试题解析
3. 下列计算中，正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{5}$ B、 $3 \sqrt{3} \times 3 \sqrt{2} = 3 \sqrt{6}$ C、 $\sqrt{27} \div \sqrt{3} = 3$ D、 $2 \sqrt{2} - \sqrt{2} = 2$

查看试题解析
4. 如图，在平行四边形ABCD中，若 $∠ B + ∠ D = 120 °$ ，则∠C的度数为（）

A、150° B、120° C、60° D、30°

查看试题解析
5. 一组数据7、9、5、11、15、11的中位数和众数是（）

A、11，8 B、11，10 C、8，11 D、10，11

查看试题解析
6. 下列图象中，y不是x的函数的是（）

A、 B、 C、 D、

查看试题解析

7. 某公司计划招聘一名公关人员，对甲、乙、丙、丁四位应试者进行了面试和笔试，他们的成绒（百分制）如表：公司决定将面试与笔试成绩按6：4的比例计算个人总分，总分最高者将被录用，则公司将录用（）

A、甲 B、乙 C、丙 D、丁

8. 在物理学中，重力的表达关系式是 $G = m g$ （G代表重力，g代表重力加速度 $g = 10 N / k g$ ， m代表物体的质量），若重力G为50N，则物体的质量m是（）

A、500 B、4 C、5 D、 $\frac{1}{5}$

查看试题解析
9. 图，在▱ABCD中，E、F、G、H分别是各边的中点，在下列3个图形中，阴影部分面积相等的是（）
①②③

A、①② B、①③ C、②③ D、①②③

查看试题解析
10. 已知 $y_{1} = a x + 1$ ， $y_{2} = - 2 x + 4$ ，当 $x < 1$ 时，总有 $y_{1} < y_{2}$ ，则a的值可以是（）

A、 $- 3$ B、3 C、 $- 1$ D、2

查看试题解析

11. 将直线 $y = 2 x - 1$ 向上平移3个单位后得到的一次函数的表达式是.

查看试题解析
12. 在三角形ABC中，D、E分别是AB、AC的中点，连接DE，若DE=4，则BC的长为.

查看试题解析
13. 如图，一个圆桶底面直径为5cm，高12cm，则桶内所能容下的最长木棒为cm.

查看试题解析
14. “ $\sqrt{a^{2}} = a$ ”是假命题，举一个反例 $a =$ .

查看试题解析
15. 若一组数据的方差为 $S^{2} = \frac{{(3 - \bar{x})}^{2} + 3 {(5 - \bar{x})}^{2} + {(6 - x)}^{2} + 2 {(8 - x)}^{2}}{7}$ ，则这组数据的众数为.

查看试题解析
16. 如图，在菱形ABCD中， $A B = \sqrt{3}$ ， $∠ A B C = 60 °$ ，点E为对角线BD上一动点（不与点B重合），且 $B E < \frac{1}{2} B D$ ，连接CE交DA延长线于点F.
① $∠ A F E = ∠ B A E$ ；

②当△AEF为直角三角形时， $B E = 2$ ；

③当△AEF为等腰三角形时， $∠ A F C = 20 °$ 或者 $∠ A F C = 40 °$ ；

④连接BF，当 $B E = C E$ 时，FC平分∠AFB.

以上结论正确的是.（填正确的序号）.

查看试题解析

17. 计算： $\sqrt{6} \div (3 \sqrt{27} - 2 \sqrt{48})$ .

查看试题解析
18. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是BD上的两点， $D E = B F$ ，连接AE，CF，求证： $A E = C F$

查看试题解析
19. 如图，直线 $l_{1}$ ： $y_{1} = 2 x + 6$ 与直线 $l_{2}$ ： $y_{2} = - x + 3$ 相交于点P.

(1)、求点P的坐标：

(2)、根据图象，求出当 $y_{1} > y_{2}$ 时，x的取值范围.

查看试题解析
20. 《九章算术》中记载：今有立木，系索其末，委地三尺，引索却行，去本八尺而索尽．问索长几何．译文：今有一竖直着的木柱，在木柱的上端系有绳索，绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺（绳索比木柱长3尺），牵着绳索退行，在距木柱底部8尺处时而绳索用尽．问绳索长是多少？

查看试题解析
21. 如图，在平行四边形ABCD中，点E为对角线BD上一点.

(1)、在边AD的上方求作一点F，使得 $E F ∥ A B$ 且 $∠ A F E = ∠ A B E$ ；
（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在（1）的条件下，连接AE，若 $∠ B A E + ∠ A E D = 180 °$ ，求证：四边形ABEF是菱形.

查看试题解析

22. 每年的3月15日是“全国反诈骗宣传日”，旨在提高人们的防范意识。为增强居民的反诈骗意识，A，B两个小区的居委会组织小区居民进行了有关反诈骗知识的有奖问答活动.现从A，B小区参加这次有奖问答活动居民的成绩中各随机抽取20个数据，分别对这20个数据进行整理、描述和分析，下面给出了部分信息：

信息一：A小区参加有奖问答活动的20名居民成绩的数据的频数分布直方图如下（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）；

A小区20名居民成绩的频数分布直方图

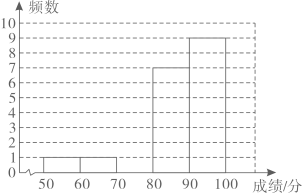
信息二：A小区参加有奖问答活动的20名居民成绩的数据在 $80 \leq x < 90$ ，这一组的是：81，82，83，85，87，88，89.

信息三：B小区参加有奖问答活动的20名居民成绩的数据如下：

分数	63	71	72	85	88	91	92	94	96	100
人数	1	3	2	3	1	3	1	4	1	1

根据以上信息，解答下列问题：

(1)、补全信息一的频数分布直方图；

(2)、A小区参加有奖问答活动的20名居民成绩的数据的中位数是；B小区参加有奖问答活动的20名居民成绩的数据的众数是；

(3)、你认为哪个小区的成绩更好？请用平均数说明理由.

23. 根据以下素材，探索完成任务.

如何利用“漏壶”探索时间
素材1	“漏壶”是一种古代计时器，数学兴趣小组根据“漏壶”的原理制作了如图①所示的液体漏壶，漏壶是由一个圆锥和一个圆柱（圆柱的最大高度是27厘米）组成的，中间连通，液体可以从圆锥容器中匀速漏到圆柱容器中，实验开始时圆柱容器中已有一部分液体.
素材2	实验记录的圆柱体容器液面高度y（厘米）与时间x（小时）的部分数据如右表所示：
问题解决
任务1	描点连线	在如图2所示的直角坐标系中描出上表的各点，用光滑的线连接；
任务2	确定关系	请确定一个合理的y与x之间函数关系式，并求出自变量x的取值范围；
任务3	拟定计时方案	小明想要设计出圆柱体容器液面高度和计时时长都是整数的计时器，且圆柱体容器液面高度需满足10厘米~20厘米，请求出所有符合要求的方案.