福建省福州市连江县2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-07-25 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 在平面直角坐标系中，点 $P (- 2 ， 3)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列说法正确的是（）

A、实数分为正实数和负实数 B、无限小数都是无理数 C、带根号的数都是无理数 D、无理数都是无限不循环小数

查看试题解析
3. 如图是某校三个年级学生人数分布扇形统计图，则七年级学生人数所占扇形的圆心角度数为（）

A、 $108 °$ B、 $120 °$ C、 $126 °$ D、 $144 °$

查看试题解析
4. 若三角形的两条边长分别为2和4，则第三边的值可能是（）

A、2 B、4 C、6 D、8

查看试题解析
5. 如果 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是关于 $x$ ， $y$ 的方程 $a x + 2 y = 6$ 的解，那么 $a$ 的值为（）

A、 $a = - 2$ B、 $a = 2$ C、 $a = - 4$ D、 $a = 4$

查看试题解析
6. 若 $a < b$ ，则下列不等式变形结果不正确的是（）

A、 $a + 3 < b + 3$ B、 $a - 3 < b - 3$ C、 $3 a < 3 b$ D、 $- \frac{a}{3} < - \frac{b}{3}$

查看试题解析
7. 如图， $A B ∥ C D$ ， $∠ A = 45 °$ ， $∠ E = 22 °$ ，则 $∠ C$ 的度数为（）

A、 $22 °$ B、 $22.5 °$ C、 $23 °$ D、 $45 °$

查看试题解析
8. 在△ABC中，AD是边BC上的中线，DE⊥AB于E，DF⊥AC于F，若AB=9，AC=6，DE=4，则线段DF的长是（）

A、4 B、6 C、9 D、12

查看试题解析
9. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条、木条剩余1尺，问木条长多少尺？如果设木条长 $x$ 尺，绳子长 $y$ 尺，那么可列方程组（）

A、 ${\begin{array}{l} y = x + 4.5 \\ 0.5 y = x - 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ y = 2 x - 1 \end{array}$ C、 ${\begin{array}{l} y = x - 4.5 \\ 0.5 y = x + 1 \end{array}$ D、 ${\begin{array}{l} y = x - 4.5 \\ y = 2 x - 1 \end{array}$

查看试题解析
10. 已知关于 $x$ 的不等式 $4 x > a$ 的负整数解是 $- 1$ 和 $- 2$ ，则 $a$ 的取值范围（）

A、 $- 12 < a < - 8$ B、 $- 12 \leq a < - 8$ C、 $- 12 < a \leq - 8$ D、 $- 12 \leq a \leq - 8$

查看试题解析

二、填空题（共6小题，每小题4分，满分24分．请在答题卡的相应位置作答）

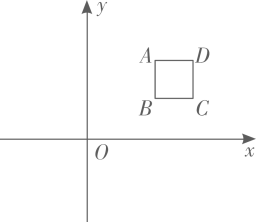
11. 调查我国中学生的视力情况，适合来用的调查方式是（填全面调查或抽样调查）

查看试题解析
12. 在 $△ A B C$ 中， $∠ A = 50 °$ ， $∠ B = ∠ C = x °$ ，则 $x$ 的值是．

查看试题解析
13. 在数轴上，与原点距离等于 $\sqrt{2}$ 的点所表示的数是．

查看试题解析
14. 如图，平面直角坐标系中，正方形 $A B C D$ 边长为1个单位长度，若 $B C ∥ x$ 轴，且点 $A$ 的坐标是 $(2 ， 2)$ ，则点 $C$ 的坐标为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $D$ ， $E$ 分别是边 $A B$ 和 $A C$ 上的两点，连接 $D E$ ，若 $∠ A = n °$ ，则 $∠ 1 + ∠ 2$ 的度数为（用含 $n$ 的式子表示）．

查看试题解析
16. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + 2 y = - a + 2 \\ 2 x - 3 y = 5 a - 3 \end{array}$ （ $a$ 是常数），若不论 $a$ 取什么实数，代数式 $k x + 2 y$ （ $k$ 是常数）的值始终不变，则 $k$ 的值为．

查看试题解析

三、解答题（本题共9小题，共86分．解答应写出文字说明、证明过程或演算步骤．）

17. 计算：

(1)、 $\sqrt[3]{- 1} + \sqrt{(- 2)^{2}} - | 2 - \sqrt{3} |$

(2)、 $\sqrt[3]{(- 3)^{3}} + \sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}})$

查看试题解析
18. 解方程组： ${\begin{array}{l} 3 x - 2 y = 5 \\ x + 4 y = 4 \end{array}$

查看试题解析
19. 解不等式 $\frac{2 y + 1}{6} \geq \frac{2 y - 5}{4} + 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
20. 在数学课上，老师提出了这样一个问题：
如图，点 $E$ 在 $A B$ 的延长线上，请从① $A B ∥ C D$ ；② $A C ∥ B D$ ；③ $∠ D B E + ∠ C = 180 °$ 中，选取两个作为题设，第三个作为结论，组成一个命题，判断其真假，并证明．

小明的做法如下：选取①②作为题设，③作为结论．即“如果 $A B ∥ C D$ ， $A C ∥ B D$ ，那么 $∠ D B E + ∠ C = 180 °$ ”是一个真命题．

证明： $∵ A B ∥ C D$

      $∴ ∠ A + ∠ C = 180 °$ （Ⅰ）

      $∵ A C ∥ B D$

      $∴ ∠ A =$       Ⅱ            （Ⅱ）

      $∴ ∠ D B E + ∠ C = 180 °$ （等量代换）

(1)、请帮助小明补全证明过程及推理依据；

(2)、请作出与小明不同的选择，组成一个新的命题，判断其真假，并证明．

查看试题解析
21. 阅读理解，并回答问题：
$∵ 4 < 5 < 9$ $∴ \sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，

$∴ \sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ．

(1)、类比上述方法，求 $\sqrt{20}$ 的整数部分和小数部分；

(2)、试判断 $\frac{\sqrt{20} - 4}{3}$ 与 $\frac{1}{3}$ 的大小，并说明理由．

查看试题解析

22. 苏联教有家苏霍姆林斯曾说过：“让学生变聪明的方法，是阅读，阅读，再阅读．”课外阅读也可以促进我们养成终身学习的习惯．某学校组织学生利用课余时间多读书，读好书，一段时间后，学校对部分学生每周阅读时间进行调查，并绘制了不完整的图表，如图所示：

阅读时间（时）	频数	所占百分比
$0 \leq x < 3$	10	10%
$3 \leq x < 6$	25	25%
$6 \leq x < 9$	$a$	30%
$9 \leq x < 12$	$b$	$c$
$12 \leq x < 15$	15	$d$

频数分布表

根据图表提供的信息，回答下列问题：

(1)、频数分布表中

a =

，

c =

；

(2)、请补全频数分布直方图；

(3)、该校共有1800名学生，请估计该校学生每周阅读时间不少于9小时的学生人数．

查看试题解析

23. 快递公司规定：寄件不超过1千克的部分按首重价格计费；寄件超过1千克的部分按续重价格计费．小林分别到甲，乙两家快递公司邮寄快递，其收费标准及实际收费情况如下表所示：

收费标准

快递公司	首重价格（元）	续重价格（元/千克）
甲公司	$a$	$b$
乙公司	$a - 3$	$b + 1$

实际收费情况

快递公司	质量（千克）	费用（元）
甲公司	2	17
乙公司	3	21

(1)、试求

a

，

b

的值；

(2)、小林想邮寄一件质量为

m (m > 1)

千克的物品，请你帮他算一算到哪家快递公司邮寄费用少？

查看试题解析

24. 在平面直角坐标系中，点 $A (a ， 2)$ 在第一象限，将点 $A$ 向左平移3个单位，再向上平移4个单位得到点 $B$ ，且点 $B$ 在第二象限，将点 $A$ 向左平移5个单位，再向下平移2个单位得到点 $C$ ．

(1)、写出点 $B$ ， $C$ 的坐标（用含 $a$ 的式子表示）；

(2)、若点 $B$ 到 $y$ 轴的距离不大于点 $A$ 到 $y$ 轴距离的2倍，求 $a$ 的取值范围；

(3)、如图，当 $a = 1$ 时，连接 $A B$ 交 $y$ 轴于 $D$ ，点 $M$ 在线段 $B D$ 上（不与点 $D$ 重合），连接 $A C$ ， $O M$ 相交于点 $N$ ，若 $S_{△ A M N} = S_{△ C O N}$ ，求点 $M$ 的横坐标．

查看试题解析
25. 在 $△ A B C$ 中， $∠ C = 90 °$ ，点 $D$ 在射线 $C B$ 上运动（点 $D$ 不与 $B$ 、 $C$ 重合），连接 $A D$ ，过点 $D$ 作 $D E ⊥ A D$ ，垂足为 $D$ ，交射线 $A B$ 于点 $E$ ．

(1)、如图1，当点 $D$ 在线段 $C B$ 上时，过点 $E$ 作 $E F ∥ A C$ 交 $C B$ 于 $F$ ．
①求证： $∠ C A D + ∠ D E F = 90 °$ ；
②如图2，作 $∠ C A D$ 的角平分线和 $∠ D E F$ 的角平分线且相交于点 $P$ ，随着点 $D$ 的运动， $∠ P$ 的度数会变化吗？如果不变，求出 $∠ P$ 的度数；如果变化，说明理由．

(2)、如图3，当点 $D$ 在线段 $C B$ 的延长线上时，过点 $E$ 作 $E F ∥ A C$ 交 $C B$ 的延长线于 $F$ ， $∠ C A D$ 的角平分线与 $∠ D E F$ 的角平分线的反向延长线相交于点 $P$ ， $∠ P$ 的度数会变化吗？请说明理由．

查看试题解析