广东省茂名市高州市2022-2023学年八年级(下)期末数学试卷
试卷更新日期:2023-07-25 类型:期末考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 围棋起源于中国,古代称之为“弈”,至今已有多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )A、
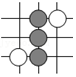 B、
B、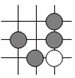 C、
C、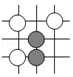 D、
D、 2. 根据下列表格对应值:
2. 根据下列表格对应值:判断关于的方程的一个解的范围是( )
A、 B、 C、 D、3. 下列等式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 要把分式方程化为整式方程,方程两边要同时乘以( )A、 B、 C、 D、5. 如图,四边形中,点 , 分别在 , 上, , 按如图方式沿着折叠,使 , 此时量得 , 则的度数是( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,已知点 , , 点是第一象限内的点,且满足是以点为直角顶点的等腰直角三角形,则点的坐标( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,已知点 , , 点是第一象限内的点,且满足是以点为直角顶点的等腰直角三角形,则点的坐标( ) A、 B、 C、 D、7. 若关于的方程有增根,则的值是( )A、 B、 C、 D、8. 某农场开挖一条米的渠道,开工后,每天比原计划多挖米,结果提前天完成任务,若设原计划每天挖米,那么求时所列方程正确的是( )A、 B、 C、 D、9. 四边形中,对角线、相交于点 , 给出下列四个条件:
A、 B、 C、 D、7. 若关于的方程有增根,则的值是( )A、 B、 C、 D、8. 某农场开挖一条米的渠道,开工后,每天比原计划多挖米,结果提前天完成任务,若设原计划每天挖米,那么求时所列方程正确的是( )A、 B、 C、 D、9. 四边形中,对角线、相交于点 , 给出下列四个条件:;;;
从中任选两个条件,能使四边形为平行四边形的选法有( )
A、种 B、种 C、种 D、种10. 一根长、宽的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后, , 则最初折叠时,的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
11. 方程 = 1的解是 .12. 分解因式 .13. 一个多边形的每个内角都是150°,那么这个多边形的边数为 .14. 如图,在四边形中,对角线平分 , , , 若点是边上一动点,则的最小值为 .
 15. 如图,在边长为的等边中,分别取三边的中点 , , , 得;再分别取三边的中点 , , , 得;这样依次下去 , 经过第次操作后得 , 则的面积为 .
15. 如图,在边长为的等边中,分别取三边的中点 , , , 得;再分别取三边的中点 , , , 得;这样依次下去 , 经过第次操作后得 , 则的面积为 .
三、计算题(本大题共1小题,共12.0分)
-
16. 大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰三角形中, , 其一腰上的高为 , 是底边上的任意一点,到腰、的距离分别为、 .
 (1)、请你结合图形来证明:;(2)、当点在延长线上时,、、之间又有什么样的结论.请你画出图形,并直接写出结论不必证明;(3)、利用以上结论解答,如图在平面直角坐标系中有两条直线: , : , 若上的一点到的距离是求点的坐标.
(1)、请你结合图形来证明:;(2)、当点在延长线上时,、、之间又有什么样的结论.请你画出图形,并直接写出结论不必证明;(3)、利用以上结论解答,如图在平面直角坐标系中有两条直线: , : , 若上的一点到的距离是求点的坐标.
四、解答题(本大题共7小题,共63.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 解不等式组 , 并把不等式组的解集在数轴上表示出来,写出不等式组的非负整数解.
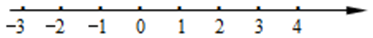 18. 先化简,再求值: , 在、0、1、2四个数中选一个合适的代入求值.19. 如图,一次函数的图象经过 , 两点.
18. 先化简,再求值: , 在、0、1、2四个数中选一个合适的代入求值.19. 如图,一次函数的图象经过 , 两点.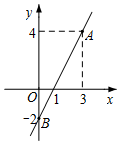 (1)、求此一次函数的解析式;(2)、结合函数图象,直接写出关于的不等式的解集.20. 如图,平行四边形中, , 点 , 分别在和的延长线上, , , .
(1)、求此一次函数的解析式;(2)、结合函数图象,直接写出关于的不等式的解集.20. 如图,平行四边形中, , 点 , 分别在和的延长线上, , , . (1)、求证:四边形是平行四边形;(2)、求的长.21. 如图,各顶点的坐标分别为 , , .
(1)、求证:四边形是平行四边形;(2)、求的长.21. 如图,各顶点的坐标分别为 , , .
⑴将向上平移个单位,再向右平移个单位,得到 , 画出平移后的图形 , 并写出平移后对应顶点的坐标;
⑵点到直线的距离 ▲ ;
⑶将绕着点顺时针旋转 , 画出旋转后的 .
22. 如图,在中, , 为边上的点.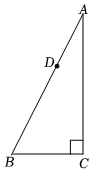 (1)、求作:平行四边形;要求:尺规作图,不写作法,保留作图痕迹(2)、在(1)所作的图形中,已知 , , , 求四边形的面积.23. 年,教育部印发义务教育课程方案和课程标准年版 , 将劳动从原来的综合实践活动课程中独立出来某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要去某菜苗基地采购 , 两种菜苗开展种植活动若购买捆种菜苗和捆种菜苗共需元;若购买捆种菜苗和捆种菜苗共需元.(1)、求菜苗基地种菜苗和种菜苗每捆的单价;(2)、学校决定用元去菜苗基地购买 , 两种菜苗共捆,菜苗基地为支持该校活动,对 , 两种菜苗均提供九折优惠求本次购买最多可购买多少捆种菜苗?
(1)、求作:平行四边形;要求:尺规作图,不写作法,保留作图痕迹(2)、在(1)所作的图形中,已知 , , , 求四边形的面积.23. 年,教育部印发义务教育课程方案和课程标准年版 , 将劳动从原来的综合实践活动课程中独立出来某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要去某菜苗基地采购 , 两种菜苗开展种植活动若购买捆种菜苗和捆种菜苗共需元;若购买捆种菜苗和捆种菜苗共需元.(1)、求菜苗基地种菜苗和种菜苗每捆的单价;(2)、学校决定用元去菜苗基地购买 , 两种菜苗共捆,菜苗基地为支持该校活动,对 , 两种菜苗均提供九折优惠求本次购买最多可购买多少捆种菜苗?
-