广东省佛山市禅城区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-25 类型:期末考试
一、单选题
-
1. 据我市气象台预报,2023年7月某日最高气温 , 最低气温 , 则当天气温(℃)的变化范围是( )A、 B、 C、 D、2. 音乐陶冶人的美.我国著名音乐家冼星海说过:“音乐是人生最大的快乐,音乐是生活中的一股清泉”,音符是传达音乐的基本元素.下列音符中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知分式( , 均为正数),若分式中每个字母的值都扩大为原来的3倍,则分式的值( )A、扩大为原来3倍 B、缩小为原来的 C、不变 D、缩小为原来的4. 下列各式中,能进行因式分解的是( )A、 B、 C、 D、5. 如图,在中, , , , 则边的长度是( )
3. 已知分式( , 均为正数),若分式中每个字母的值都扩大为原来的3倍,则分式的值( )A、扩大为原来3倍 B、缩小为原来的 C、不变 D、缩小为原来的4. 下列各式中,能进行因式分解的是( )A、 B、 C、 D、5. 如图,在中, , , , 则边的长度是( )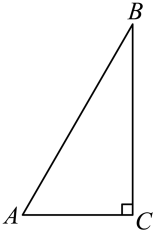 A、3 B、4 C、 D、6. 在中, , 则的度数是( )A、 B、 C、 D、7. 如图,直线经过点和点 , 则关于的不等式的解集是( )
A、3 B、4 C、 D、6. 在中, , 则的度数是( )A、 B、 C、 D、7. 如图,直线经过点和点 , 则关于的不等式的解集是( ) A、 B、 C、 D、8. 若 (b≠0),则 =( )A、0 B、 C、0或 D、1或 29. 如图,在中, , , 是的中垂线,则的周长为( )
A、 B、 C、 D、8. 若 (b≠0),则 =( )A、0 B、 C、0或 D、1或 29. 如图,在中, , , 是的中垂线,则的周长为( ) A、10 B、11 C、12 D、1310. 体育锻炼能促进青少年享受乐趣、增强体质、健全人格、锻炼意志.某校积极开展“阳光体育”活动.在一次体育活动中,小超和小明进行1000米测试,小超的速度是小明的1.25倍,小超比小明快30秒到达终点.若设小明的速度是米/秒,则所列方程正确的是( )A、 B、 C、 D、
A、10 B、11 C、12 D、1310. 体育锻炼能促进青少年享受乐趣、增强体质、健全人格、锻炼意志.某校积极开展“阳光体育”活动.在一次体育活动中,小超和小明进行1000米测试,小超的速度是小明的1.25倍,小超比小明快30秒到达终点.若设小明的速度是米/秒,则所列方程正确的是( )A、 B、 C、 D、二、填空题
-
11. 若分式有意义,则满足的条件是 .12. 因式分解: .13. “岭南四大名园”之一的佛山“梁园”里不仅有秀水、奇石、名帖,还有随处可见的古典窗棂(如图①所示),这也是岭南建筑艺术之一、图②是这种窗棂中的部分图案.其中、、、是五边形的4个外角,若 , 则的度数是 .
 14. 如图,点、在直线上,为直线外一点,连接 , 分别以点、为圆心,、的长为半径画弧,两弧交于点 , 连接、 , 则可以判定四边形是平行四边形的理由是 .
14. 如图,点、在直线上,为直线外一点,连接 , 分别以点、为圆心,、的长为半径画弧,两弧交于点 , 连接、 , 则可以判定四边形是平行四边形的理由是 .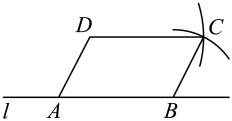 15. 如图,将形状大小完全相同的“○”按照一定的规律(如下图所示)摆放,其中图①的“○”的个数为 , 图②中的“○”的个数为 , 图③中的“○”的个数为 , ……以此类推,则的值是 . (为正整数)
15. 如图,将形状大小完全相同的“○”按照一定的规律(如下图所示)摆放,其中图①的“○”的个数为 , 图②中的“○”的个数为 , 图③中的“○”的个数为 , ……以此类推,则的值是 . (为正整数)
三、解答题
-
16. 解不等式组:17. 先化简,再求值: , 并在1,2,3中选择一个合适的值代入求值.18. 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,的顶点都在格点上.

⑴将向右平移6个单位长度得到 , 请画出;
⑵画出关于点的中心对称图形 .
19. 角平分线的性质定理“角平分线上的点到角两边的距离相等.”是一条常用定理,灵活应用这个定理解决实际问题,往往能起到事半功倍的效果;如图,在中, , , 是的角平分线. (1)、若 , 求的长;(2)、判断、、之间的数量关系,并说明理由.20. 阅读塑造精神,阅读滋养情感,阅读增长智慧.在“书香校园”的系列活动中,某校计划购进一批图书.已知购买2本科技类图书和3本文学类图书共需156元,购买4本科技类图书和5本文学类图书共需284元.(1)、每本科技类图书与每本文学类图书的价格分别为多少元?(2)、学校计划购进科技类图书和文学类图书共60本,且总费用不超过2100元,那么最多可购进科技类图书多少本?21. 已知,如图,点、、、在同一条直线上, , , . 求证:
(1)、若 , 求的长;(2)、判断、、之间的数量关系,并说明理由.20. 阅读塑造精神,阅读滋养情感,阅读增长智慧.在“书香校园”的系列活动中,某校计划购进一批图书.已知购买2本科技类图书和3本文学类图书共需156元,购买4本科技类图书和5本文学类图书共需284元.(1)、每本科技类图书与每本文学类图书的价格分别为多少元?(2)、学校计划购进科技类图书和文学类图书共60本,且总费用不超过2100元,那么最多可购进科技类图书多少本?21. 已知,如图,点、、、在同一条直线上, , , . 求证: (1)、(2)、四边形是平行四边形.22. 我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微”.请你利用“数形结合”的思想解决以下问题.如图1,边长为的正方形中有一个边长为的小正方形,图2题由图1外阴影部分排成的一个长方形,设图1中阴影部分面积为 , 图2中阴影部分面积为 .
(1)、(2)、四边形是平行四边形.22. 我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微”.请你利用“数形结合”的思想解决以下问题.如图1,边长为的正方形中有一个边长为的小正方形,图2题由图1外阴影部分排成的一个长方形,设图1中阴影部分面积为 , 图2中阴影部分面积为 . (1)、请直接用含和的代数式表示 , ;写出利用图形的面积关系所得到的公式:(用式子表达).(2)、请依据(1)得到的公式计算: .(3)、请用(1)中的公式证明任意两个相邻奇数的平方差必是8的倍数.23. 如图1,在中, , , 点 , 分别在边 , 上, , 连接 , , 点 , , 分别为 , , 的中点.
(1)、请直接用含和的代数式表示 , ;写出利用图形的面积关系所得到的公式:(用式子表达).(2)、请依据(1)得到的公式计算: .(3)、请用(1)中的公式证明任意两个相邻奇数的平方差必是8的倍数.23. 如图1,在中, , , 点 , 分别在边 , 上, , 连接 , , 点 , , 分别为 , , 的中点. (1)、线段与的数量关系是 , 位置关系是;(2)、把绕点顺时针方向旋转到图2的位置,连接 , , , 判断的形状,并说明理由;(3)、若 , , 绕点在平面内旋转过程中,请直接写出的面积取得最大值时的长.
(1)、线段与的数量关系是 , 位置关系是;(2)、把绕点顺时针方向旋转到图2的位置,连接 , , , 判断的形状,并说明理由;(3)、若 , , 绕点在平面内旋转过程中,请直接写出的面积取得最大值时的长.