广东省深圳市福田区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-25 类型:期末考试
一、单选题
-
1. 2023年6月4日6时33分,神舟十五号载人飞船返回舱在东风着陆场平安着陆,神舟十五号载人飞行任务取得圆满成功,展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上用阴影表示正确的是( )A、
2. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 五边形的内角和为( )A、360° B、540° C、720° D、900°5. 下列命题中,属于真命题的是( )A、多边形的外角和都等于 B、直角三角形角的对边等于另一直角边的一半 C、一组对边相等的四边形是平行四边形 D、等腰三角形的高、中线、角平分线重合6. 如图,绕点顺时针旋转到的位置.如果 , 那么等于( )
4. 五边形的内角和为( )A、360° B、540° C、720° D、900°5. 下列命题中,属于真命题的是( )A、多边形的外角和都等于 B、直角三角形角的对边等于另一直角边的一半 C、一组对边相等的四边形是平行四边形 D、等腰三角形的高、中线、角平分线重合6. 如图,绕点顺时针旋转到的位置.如果 , 那么等于( )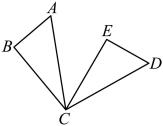 A、 B、 C、 D、7. 如图,中, , 分别以点和点为圆心,以大于的长为半径作弧,两弧相交于点和点 , 作直线 , 分别交 , 于点和点 . 若 , , 则的长为( )
A、 B、 C、 D、7. 如图,中, , 分别以点和点为圆心,以大于的长为半径作弧,两弧相交于点和点 , 作直线 , 分别交 , 于点和点 . 若 , , 则的长为( ) A、 B、 C、 D、8. 如图,平行四边形中,平分 , . 若 , , 则的长为( )
A、 B、 C、 D、8. 如图,平行四边形中,平分 , . 若 , , 则的长为( ) A、13 B、17 C、18 D、259. 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为米/秒,下列方程正确的是( )A、 B、 C、 D、10. 如图,在四边形中, , , , , , 则的长度为( )
A、13 B、17 C、18 D、259. 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为米/秒,下列方程正确的是( )A、 B、 C、 D、10. 如图,在四边形中, , , , , , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 当时,分式的值为0.12. 若 , , 则的值为13. 如图,等腰中,为底边上的高,点为的中点.若 , 则
 14. 如图,已知函数(为常数)和(为常数且)的图象交于点 , 则关于的不等式的解集是
14. 如图,已知函数(为常数)和(为常数且)的图象交于点 , 则关于的不等式的解集是 15. 为了让学生更直观地认识等腰直角三角形,林老师制作了一个等腰直角三角形教具,课余时间他把教具挂在墙上.如图,教具中, , , 点 , , 位于同一平面内,这三个顶点到地面的距离分别为 , , , 则的长为 .
15. 为了让学生更直观地认识等腰直角三角形,林老师制作了一个等腰直角三角形教具,课余时间他把教具挂在墙上.如图,教具中, , , 点 , , 位于同一平面内,这三个顶点到地面的距离分别为 , , , 则的长为 .
三、解答题
-
16. 因式分解:(1)、;(2)、 .17. 解不等式组 , 并写出不等式组的非负整数解.18. 先化简,再求值 , 其中 .19. 已知三个顶点的坐标分别为 , , .
 (1)、作关于点成中心对称的(点的对应点为 , 点的对应点为);(2)、把向右平移3个单位,作出平移后的(点的对应点为 , 点的对应点为 , 点的对应点为);(3)、轴上存在点 , 使得的值最小,则点的坐标是20. 如图,已知四边形中,交于点 , , , 延长到点 , 使 , 连接 .
(1)、作关于点成中心对称的(点的对应点为 , 点的对应点为);(2)、把向右平移3个单位,作出平移后的(点的对应点为 , 点的对应点为 , 点的对应点为);(3)、轴上存在点 , 使得的值最小,则点的坐标是20. 如图,已知四边形中,交于点 , , , 延长到点 , 使 , 连接 . (1)、求证:四边形是平行四边形;(2)、若 , , , 求的周长.21. 【综合与实践】生活中,我们所见到的地面、墙面、服装面料等,上面的图案常常是由一种或几种形状相同的图形拼接而成的.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,就是平面图形的镶嵌.
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的周长.21. 【综合与实践】生活中,我们所见到的地面、墙面、服装面料等,上面的图案常常是由一种或几种形状相同的图形拼接而成的.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,就是平面图形的镶嵌.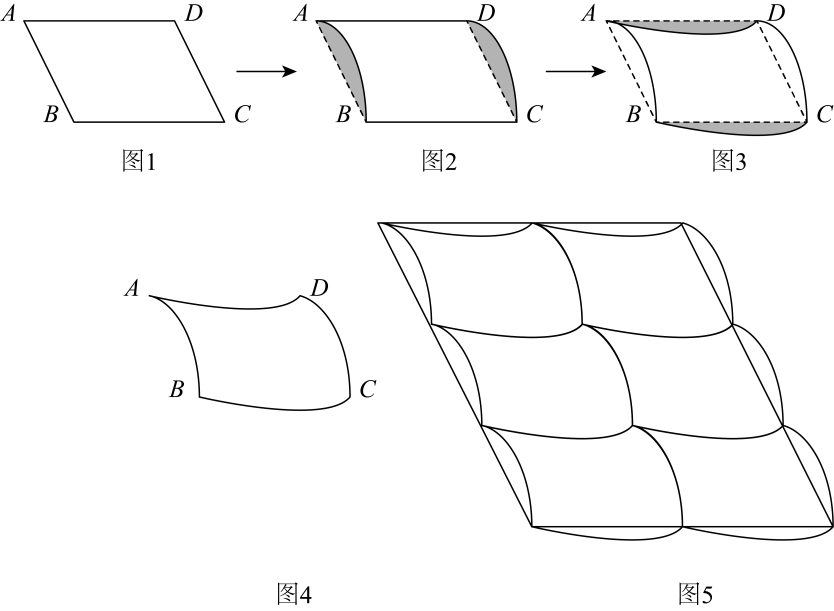
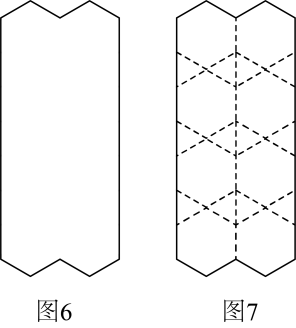 (1)、如图1,在中, , , , 图2右侧的阴影部分可以看成是左侧阴影部分沿射线方向平移而成,其中,平移的距离是 . 同理,再进行一次切割平移,可得图3,即图4可以看成由平行四边形经过两次切割平移而成.我们可以用若干个如图4所示的图形,平面镶嵌成如图5的图形,则图5的面积是(2)、小明家浴室装修,在墙中央留下了如图6所示的空白,经测量可以按图7所示,全部用边长为1的正三角形瓷砖镶嵌.小明调查后发现:一块边长为1的正三角形瓷砖比一块边长为1的正六边形瓷砖便宜40元;用500元购买正三角形瓷砖与用2500元购买正六边形瓷砖的数量相等.
(1)、如图1,在中, , , , 图2右侧的阴影部分可以看成是左侧阴影部分沿射线方向平移而成,其中,平移的距离是 . 同理,再进行一次切割平移,可得图3,即图4可以看成由平行四边形经过两次切割平移而成.我们可以用若干个如图4所示的图形,平面镶嵌成如图5的图形,则图5的面积是(2)、小明家浴室装修,在墙中央留下了如图6所示的空白,经测量可以按图7所示,全部用边长为1的正三角形瓷砖镶嵌.小明调查后发现:一块边长为1的正三角形瓷砖比一块边长为1的正六边形瓷砖便宜40元;用500元购买正三角形瓷砖与用2500元购买正六边形瓷砖的数量相等.①请问两种瓷砖每块各多少元?
②小明对比两种瓷砖的价格后发现:用若干块边长为1的正三角形瓷砖和边长为1的正六边形瓷砖一起镶嵌总费用会更少.按小明的想法,将空白处全部镶嵌完,购买瓷砖最少需要 ▲ 元.
22. 在等腰中, , 点是射线上的动点,垂直于直线于点 , 交直线于点 . (1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为
(1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为