广东省深圳市坪山区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-07-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列深圳交通的标志图案中，是轴对称图形的是（）

A、深圳巴士 B、深圳东部公交 C、深圳航空 D、深圳地铁

查看试题解析
2. 红细胞是血液中数量最多的一种血细胞，它将氧气从肺送到身体各个组织，它的直径约为 $0.0000078 m$ ，将 $0.0000078$ 用科学记数法表示为（）

A、 $78 \times 1 0^{- 7}$ B、 $7.8 \times 1 0^{- 7}$ C、 $7.8 × 1 0^{- 6}$ D、 $0.78 \times 1 0^{- 6}$

查看试题解析
3. 桌上倒扣着背面图案相同的5张扑克牌，其中3张黑桃，2张红桃，从中随机抽取3张，下列事件是不可能事件的是（）

A、摸出三张黑桃 B、摸出三张红桃 C、摸出一张黑桃 D、摸出一张红桃

查看试题解析
4. 下列计算正确的是（）

A、 $a^{6} \div a^{3} ＝ a^{2}$ B、 $(- 2 a)^{3} ＝ - 8 a^{3}$ C、 $(3 a^{2})^{2} ＝ 6 a^{4}$ D、 $a^{3} • a^{2} ＝ a^{6}$

查看试题解析
5. 计算 $(x + 1) (x - 1) =$ （）

A、 $x^{2} + 1$ B、 $x^{2} - 1$ C、 $2 x - 1$ D、 $2 x + 1$

查看试题解析
6. 下列说法中，正确的是（）

A、三角形任意两边之差小于第三边 B、三角形的一条角平分线将三角形分成两个面积相等的三角形 C、两边和其中一边的对角分别相等的两个三角形全等 D、三角形的三条高都在三角形内部

查看试题解析
7. 如图，某人沿路线 $A \to B \to C \to D$ 行走， $A B$ 与 $C D$ 方向相同， $∠ 1 = 128 °$ ，则 $∠ 2 =$ （）

A、 $52 °$ B、 $118 °$ C、 $128 °$ D、 $138 °$

查看试题解析
8. 小王上学时以每小时 $6 k m$ 的速度行走，他所走的路程 $s (k m)$ 与时间 $t (h)$ 之间的关系为： $s = 6 t$ ，则下列说法正确的是（）

A、s、t和6都是变量 B、s是常量，6和t是变量 C、6是常量，s和t是变量 D、t是常量，6和s是变量

查看试题解析
9. 如图，已知 $A B ∥ D E$ ， $B E = C F$ ，请你添加一个条件（），使得 $△ A B C ≌ △ D E F$ ．

A、 $A C = D F$ B、 $A B = D E$ C、 $B C = E F$ D、 $∠ D E C = ∠ A C B$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，利用尺规在 $B C ， B A$ 上分别截取 $B E ， B D$ ，使 $B E = B D$ ，分别以D，E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ C B A$ 内交于点F，作射线 $B F$ 交 $A C$ 于点G，若 $A C = 9 ， A G = 5$ ，过点G作 $G P ⊥ A B$ 交 $A B$ 于点P，则 $G P$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 计算2a·3a= .

查看试题解析
12. 某景区在端午节期间，门票售价为每人100元，设节日期间共接待游客x人，门票的总收入为y（元），则y与x之间的关系可表示为．

查看试题解析
13. 如果三角形的一个内角等于另外两个内角的和，那么这个三角形是三角形.

查看试题解析
14. 如图，直线 $a ∥ b$ ，点A在直线a上，点B在直线b上， $A C = B C$ ， $∠ C = 110 °$ ， $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
15. ^.如图，在等腰 $△ A B C$ 中，AB=AC=11，BC=8，∠A=40°，等腰 $△ D E F$ 中，DE=DF=5，∠EDF=70°，则 $△ C D F$ 周长为．

查看试题解析

三、解答题

16. 计算： $2^{0} - 3 + {(\frac{1}{3})}^{- 1} + 4$ ．

查看试题解析
17. 先化简，再求值： ${(x - 1)}^{2} + 2 x - 1$ ，其中x＝3．

查看试题解析
18. 在一个口袋中只装有4个白球和6个红球，它们除颜色外完全相同．

(1)、“从口袋中随机摸出一个球是红球”发生的概率是；

(2)、现从口袋中取走若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是 $\frac{4}{5}$ ，求取走了多少个红球？

查看试题解析
19. 把下列说理过程补充完整：
如图， $∠ D E H + ∠ E H G = 180 °$ ， $∠ 1 = ∠ 2$ ， $∠ C = ∠ A$ ，请说明 $∠ A E H = ∠ F$ ．

说明理由为：因为 $∠ D E H + ∠ E H G = 180 °$ ，

所以 $E D ∥$       ▲       ，（）

则 $∠ 1 = ∠ C$ ．（）

      $∠ 2 =$       ▲      （两直线平行，内错角相等）

又因为 $∠ 1 = ∠ 2$ ，所以 $∠ C =$       ▲       ，

又因为 $∠ C = ∠ A$ ，

所以 $∠ A =$       ▲       ，

所以 $A B ∥ D F$ ，（）

所以 $∠ A E H = ∠ F$ ．（）

查看试题解析
20. 如图是某市一天的气温变化图，在这一天中，气温随着时间变化而变化，请观察图象，回答下列问题：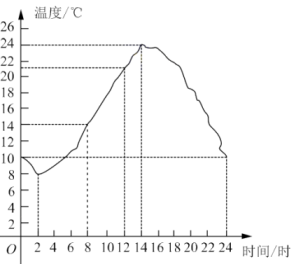

(1)、在这一天中（凌晨0时到深夜24时均在内），气温在时达到最低，最低气温是℃，气温在时达到最高；

(2)、上午8时的气温是℃，下午14时的气温是℃；

(3)、在什么范围内这天的气温在下降的？这天从2时到14时气温上升了多少？

查看试题解析
21. 如图1，在正方形网格上有一个 $△ A B C$ ， A、B、C三点都在格点上．

(1)、在图1中画出 $△ A B C$ 关于直线 $M N$ 的对称图形 $△ A_{1} B_{1} C_{1}$ ；（不写画法）

(2)、若网格上的每个小正方形方格的边长为1，则 $△ A B C$ 的面积为多少？

(3)、如图2，若直线 $M N$ 上有一动点P﹐连接 $P A 、 P B$ ﹐求当 $P A ＋ P B$ 取最小值时 $△ P A B$ 的面积．

查看试题解析
22. 在 $△ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ．

(1)、【特例感知】
如图1，如果 $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D， $C E ⊥ B D$ ，垂足E在 $B D$ 的延长线上，则线段 $C E$ 和 $B D$ 有怎样的数量关系？请说明理由；

(2)、【问题探究】
如图2，点D是边 $A C$ 上一点，连接 $B D$ ，过点A作 $A E ⊥ B D$ 于点E，过点C作 $C F ⊥ B D$ ，交 $B D$ 的延长线于点F，则线段 $B F 、 A E$ 和 $C F$ 有怎样的数量关系？请说明理由；

(3)、【拓展应用】
如图3，点D是边 $A C$ 上一点，连接 $B D$ ，过点C作 $C E ⊥ B D$ ，交 $B D$ 的延长线于点E，连接 $A E$ ，若 $A E = 6$ ，则 $S_{Δ A B D} - S_{Δ C D E} =$ ．

查看试题解析