2023-2024学年初中数学七年级上册3.1 从算式到方程 同步分层训练基础卷 (人教版吉林地区)
试卷更新日期:2023-07-25 类型:同步测试
一、选择题
-
1. 根据等式的性质,下列变形不成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则2. 小明以每小时4千米的速度从家步行到学校上学,放学时以每小时3千米的速度按原路返回,结果发现比上学所花的时间多10分钟,如果设上学路上所花的时间为x小时,根据题意所列方程正确的是( )A、 B、 C、 D、3. 我国古代数学著作《孙子算经》卷中记载“多人共车”问题,原文如下:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:今有若干人乘车,每3人乘1车,最终剩余2辆车;若每2人共乘1车,最终剩余9个人无车可乘,问有多少人,多少辆车?设有x个人,根据题意列方程正确的是( )A、 B、 C、 D、4. 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,可列出的方程为( )A、 B、 C、 D、5. 已知关于x的一元一次方程的解是 , 关于y的一元一次方程的解是(其中b和c是含有y的代数式),则下列结论符合条件的是( )A、 B、 C、 D、6. 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 , 这时增加了乙队,两队又共同工作了半个月,总工程全部完成,如果乙队单独完成总工程需多少个月?设乙队单独完成总工程共需个月,则下列方程正确的是( )A、 B、 C、 D、7. 下面各选项中运用等式的性质进行的变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么8. 《孙子算经》中有一道题,原文是:今有四人共车,一车空;三人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每4人共乘一车,最终剩余1辆车;若每3人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、
二、填空题
-
9. 关于x的方程2(x-1)-a=0的根是3,则a的值是.10. 若是关于的方程的解,则.11. 已知是关于x的一元一次方程,则m的值是.12. 关于的方程的解是 , 则的值是.13. 如图,小红同学编了一道数学谜题,若设“□”内的数字为x,则可列出方程为.
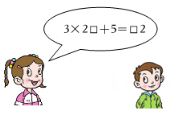
三、计算题