2023-2024学年初中数学七年级上册2.2 整式的加减同步分层训练培优卷 (人教版吉林地区)

试卷更新日期：2023-07-25 类型：同步测试

进入出卷网下载

一、选择题

1. 下列合并同类项中，正确的是（　　）

A、 $2 x + 3 y = 5 x y$ B、 $3 x^{2} + 2 x^{3} = 5 x^{5}$ C、 $- 2 x^{2} + 2 x^{2} = x^{2}$ D、 $x^{2} - 3 x^{2} = - 2 x^{2}$

查看试题解析
2. 已知数a，b，c在数轴上的位置如图所示，化简|a+b|-|a-b|+|c-a|的结果为（）

A、-3a+c B、a-2b-c C、-a-2b+c D、-a+2b+c

查看试题解析
3. 下列运算中，正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ C、 $5 a^{2} - 4 a^{2} = 1$ D、 $3 a^{2} b - 3 b a^{2} = 0$

查看试题解析
4. 关于多项式3x²-y-3xy³+x⁵-1，下列说法错误的是（　　）

A、这个多项式是五次五项式 B、常数项是-1 C、四次项的系数是3 D、按x降幂排列为x⁵+3x²-3xy³-y-1

查看试题解析
5. 下面计算正确的是（）

A、 $3 x^{2} y - 2 y^{2} x = x y$ B、 $a b - \frac{b a}{2} = \frac{1}{2} a b$ C、 $2 a^{2} + a = 3 a^{3}$ D、 $m^{4} + m^{4} = m^{8}$

查看试题解析
6. 下列两个数互为相反数的是（）

A、3和 $\frac{1}{3}$ B、 $- (- 3)$ 和 $| - 3 |$ C、 ${(- 3)}^{2}$ 和 $- 3^{2}$ D、 ${(- 3)}^{3}$ 和 $- 3^{3}$

查看试题解析
7. 为求1+2+2²+2³+…+2²⁰¹⁵的值，可令S=1+2+2²+2³+…+2²⁰¹⁵ ，则2S=2+2²+2³+…+2²⁰¹⁶ ，因此2S﹣S=2²⁰¹⁶﹣1.仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁵的值为（）

A、5²⁰¹⁵﹣1 B、5²⁰¹⁶﹣1 C、 $\frac{5^{2015} - 1}{4}$ D、 $\frac{5^{2016} - 1}{4}$

查看试题解析
8. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，且 $| c | > | a | > | b |$ ，则 $| a + b | - 2 | c - b | + | a + c | =$ （）．

A、 $c - b$ B、0 C、 $3 b - 3 c$ D、 $2 a + 3 b - c$

查看试题解析

二、填空题

9. 如果有理数a、b、c在数轴上的位置如图所示，则 $| a + b | - | b - 1 | - | a - c | =$ .

查看试题解析
10. 已知a，b，c三个有理数在数轴上对应的位置如图所示，化简|c-a|-|a-b|-|b|＝.

查看试题解析
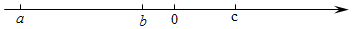11. 若关于a，b的多项式 $5 (a^{2} - 2 a b + b^{2}) - (a^{2} + m a b - b^{2})$ 中不含有 $a b$ 项，则m= ．

查看试题解析
12. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“英华数”，定义新运算：将一个“英华数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω （ 27 ）$ ．

(2)、若m，n都是“英华数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析
13. 如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形 $A B C D$ ，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积 $S_{1}$ 与（2）图长方形的面积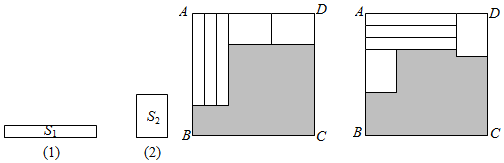 $S_{2}$ 的比是.

查看试题解析

三、计算题

14. 先化简，再求值：6xy²-4x²y-3（xy²- $\frac{2}{3}$ x²y），其中x＝2，y＝-1.

查看试题解析

四、解答题

15. 先化简，再求值： $9 (\frac{1}{9} x^{2} - \frac{2}{3} x + 1) - 4 (\frac{1}{4} x^{2} + x + 2) - 10$ ，其中 $x = 3$ .

查看试题解析
16. 先化简，再求值： $(3 a^{2} + 6 a - 1) - 2 (a^{2} + 2 a - 3)$ .其中 $a = - 2$ .

查看试题解析

五、综合题

17. 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $x$ 台电子产品， $y$ 个配件 $(y > x > 0)$ .

(1)、分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）

(2)、若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？

查看试题解析
18. 如图，数轴上的点A，B，C分别表示有理数a，b，c，其中b是最小的正整数，且a，b，c满足(c-5)²+|a+b|=0．

(1)、a= ， b= ， c=

(2)、P为线段BC上的一个动点，点P表示的数为x，化简：|x-b|-|x-c|．

(3)、点A，B，C开始在数轴上运动，点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和每秒5个单位长度的速度向右运动，t秒后，我们用AB表示点A与点B之间的距离，用BC表示点B与点C之间的距离．探究：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求出BC-AB的值．

查看试题解析

2023-2024学年初中数学七年级上册2.2 整式的加减 同步分层训练培优卷 (人教版吉林地区)

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023-2024学年初中数学七年级上册2.2 整式的加减同步分层训练培优卷 (人教版吉林地区)