江苏省南京市玄武区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-25 类型:期末考试
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 干燥空气中,各组分气体的体积分数大约是:氮气78%,氧气21%,稀有气体0.94%,二氧化碳0.03%,其他气体和杂质0.03%,为反映空气中各组分气体的体积所占的百分比,最合适的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图3. 下列二次根式的计算中,正确的是( )A、 B、 C、 D、4. 若分式中的和都扩大为原来的3倍后,分式的值不变,则A可能是( )A、 B、 C、 D、35. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A、1个 B、2个 C、3个 D、4个2. 干燥空气中,各组分气体的体积分数大约是:氮气78%,氧气21%,稀有气体0.94%,二氧化碳0.03%,其他气体和杂质0.03%,为反映空气中各组分气体的体积所占的百分比,最合适的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图3. 下列二次根式的计算中,正确的是( )A、 B、 C、 D、4. 若分式中的和都扩大为原来的3倍后,分式的值不变,则A可能是( )A、 B、 C、 D、35. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )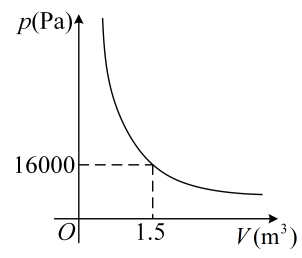 A、不小于 B、不大于 C、不小于 D、不大于6. 如图,正方形和正方形的对称中心都是点 , 其边长分别是3和2,则图中阴影部分的面积是( )
A、不小于 B、不大于 C、不小于 D、不大于6. 如图,正方形和正方形的对称中心都是点 , 其边长分别是3和2,则图中阴影部分的面积是( )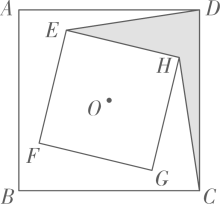 A、 B、1.25 C、1.5 D、无法确定
A、 B、1.25 C、1.5 D、无法确定二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
-
7. 若代数式有意义,则的取值范围是.8. 已知反比例函数的图像在第二、第四象限,则的取值范围是.9. 在一副扑克牌中,任意抽取一张,则下列事件:①抽到“红桃”;②抽到“黑桃A”;③抽到“K”;④抽到“红色的”,则事件发生的可能性最大的是.(填序号)10. 某校篮球队进行篮球训练,某队员投篮的统计结果如下表.根据表中数据可知该队员一次投篮命中的概率的估计值是(精确到0.01)
投篮次数
10
50
100
150
200
500
1000
2000
命中次数
9
41
72
108
143
361
722
1442
命中率
0.900
0.820
0.720
0.720
0.715
0.722
0.722
0.721
11. 举一个反例说明“”是不成立的,则的值可以是.12. 写一个一元二次方程: , 使其满足:二次项系数为2,且两根分别是2,.13. 如图,的对角线 , 交于点O,E,F分别是 , 的中点.若 , 的周长是 , 则的长为.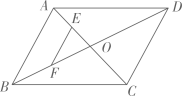 14. 关于的分式方程的解为正数,则的取值范围是.15. 如图,反比例函数的图像经过菱形的顶点 , 点在轴上,过点作轴的垂线与反比例函数的图象相交于点.若 , 则点的坐标是.
14. 关于的分式方程的解为正数,则的取值范围是.15. 如图,反比例函数的图像经过菱形的顶点 , 点在轴上,过点作轴的垂线与反比例函数的图象相交于点.若 , 则点的坐标是.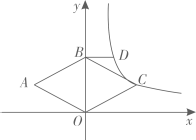 16. 如图,在矩形中, , , 是边上的动点,连接 , 将绕点逆时针旋转90°得到 , 连接 , 则的最小值为.
16. 如图,在矩形中, , , 是边上的动点,连接 , 将绕点逆时针旋转90°得到 , 连接 , 则的最小值为.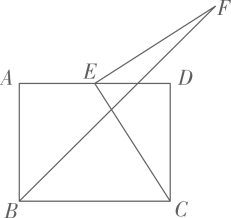
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
-
17. 计算:(1)、;(2)、.18. 解分式方程:(1)、;(2)、.19. 解一元二次方程:(1)、;(2)、.20. 先化简,再求值: , 其中.21. 第19届亚运会将于2023年9月23日至10月8日在杭州举行.本届亚运会赛事项目共有4个大类,分别是竞技性比赛、球类比赛、对抗性比赛和水上比赛.某体育爱好小组的同学想了解该校学生最喜爱的赛事项目,且只能选择一项.随机抽取了部分学生进行调查并统计结果,绘制了如下尚不完整的扇形统计图和条形统计图.
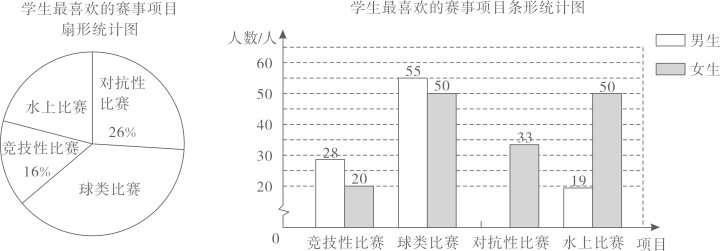 (1)、本次调查的样本容量为;扇形统计图中,“水上比赛”所对应扇形的圆心角为;(2)、将条形统计图补充完整;(3)、若该校共有2500名学生,请估计该校最喜爱“球类比赛”学生的人数.22. 某漆器厂接到制作640件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多60%,结果提前6天完成任务,原来每天制作多少件?23. 如图,在中, , D、E分别是、的中点,过点作 , 交延长线于点 , 连接、.
(1)、本次调查的样本容量为;扇形统计图中,“水上比赛”所对应扇形的圆心角为;(2)、将条形统计图补充完整;(3)、若该校共有2500名学生,请估计该校最喜爱“球类比赛”学生的人数.22. 某漆器厂接到制作640件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多60%,结果提前6天完成任务,原来每天制作多少件?23. 如图,在中, , D、E分别是、的中点,过点作 , 交延长线于点 , 连接、.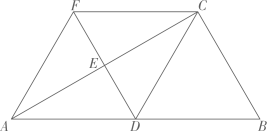 (1)、求证:四边形是菱形;(2)、当时,四边形是正方形.24. 如图,反比例函数的图象与一次函数的图象交于点 , .
(1)、求证:四边形是菱形;(2)、当时,四边形是正方形.24. 如图,反比例函数的图象与一次函数的图象交于点 , .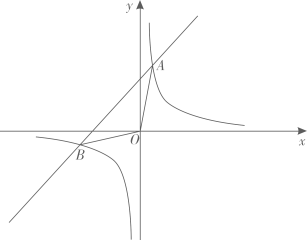 (1)、若 , 求与的值;(2)、关于的不等式的解集为;(3)、连接 , , 若的面积为12,则的值为.25. 已知菱形.
(1)、若 , 求与的值;(2)、关于的不等式的解集为;(3)、连接 , , 若的面积为12,则的值为.25. 已知菱形.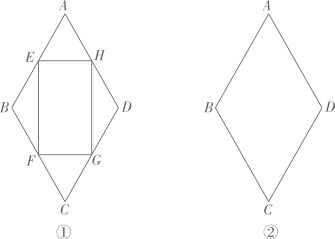 (1)、如图①,E,F,G,H分别是AB,BC,CD,DA的中点,求证:四边形是矩形.(2)、在图②中,仅用无刻度直尺作矩形 , 使其顶点E,F,G,H分别在边AB,BC,CD,DA上.26. 如图①,在四边形中,若 , 且 , 则称四边形为“完美筝形”.
(1)、如图①,E,F,G,H分别是AB,BC,CD,DA的中点,求证:四边形是矩形.(2)、在图②中,仅用无刻度直尺作矩形 , 使其顶点E,F,G,H分别在边AB,BC,CD,DA上.26. 如图①,在四边形中,若 , 且 , 则称四边形为“完美筝形”.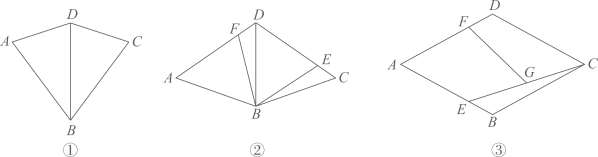 (1)、下列四边形中,一定是“完美筝形”的是____.A、正方形 B、对角线夹角是60°的矩形 C、菱形 D、有一个内角是60°的菱形(2)、如图②,在“完美筝形”中, , 且 , E,F分别是 , 上的点,且 , 求证:;(3)、如图③,在菱形中, , , E,F分别是 , 上的动点(与A,B,D都不重合),且 , 若是的中点,连接 , 则的取值范围是.27. 对于两个不同的函数,通过加法运算可以得到一个新函数,我们把这个新函数称为两个函数的“和函数”.例如:对于函数和 , 则函数 , 的“和函数”.
(1)、下列四边形中,一定是“完美筝形”的是____.A、正方形 B、对角线夹角是60°的矩形 C、菱形 D、有一个内角是60°的菱形(2)、如图②,在“完美筝形”中, , 且 , E,F分别是 , 上的点,且 , 求证:;(3)、如图③,在菱形中, , , E,F分别是 , 上的动点(与A,B,D都不重合),且 , 若是的中点,连接 , 则的取值范围是.27. 对于两个不同的函数,通过加法运算可以得到一个新函数,我们把这个新函数称为两个函数的“和函数”.例如:对于函数和 , 则函数 , 的“和函数”.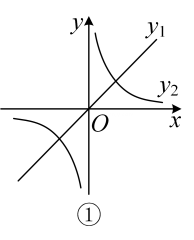 (1)、已知函数和 , 这两个函数的“和函数”记为.
(1)、已知函数和 , 这两个函数的“和函数”记为.①写出的表达式,并求出当x取何值时,的值为;
②函数 , 的图像如图①所示,则的大致图像是 ▲ .
A.
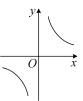 B.
B.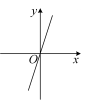 C.
C.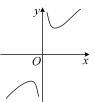 D.
D.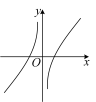 (2)、已知函数和 , 这两个函数的“和函数”记为.
(2)、已知函数和 , 这两个函数的“和函数”记为.①下列关于“和函数”的性质,正确的有 ▲ ;(填写所有正确的选项)
A.的图像与x轴没有公共点
B.的图像关于原点对称
C.在每一个象限内,随x的值增大而减小
D.当时,随着x的值增大,的图像越来越接近的图像
②探究函数与一次函数(为常数,且图像的公共点的个数及对应的k的取值范围,直接写出结论.