江苏省南通市如东县2022-2023学年七年级下册数学第二次月考试卷
试卷更新日期:2023-07-25 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列长度的三条线段能组成三角形的是( )A、6,5,10 B、5,3,2 C、5,8,14 D、6,9,22. 8的立方根是( )A、 B、 C、 D、3. 以下调查中,适宜采用全面调查的是( )A、了解某品牌某一批次汽车刹车系统的使用寿命 B、了解一批新型节能灯泡的使用寿命 C、了解某校七年级一班学生对如东县第六届“金牛奖”的获奖情况的知晓率 D、了解南通电视台城市日历收视率4. 已知 , 则下列变形错误的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点的坐标为如果把点向左平移个单位,再向上平移个单位得到点 , 则的坐标为( )A、 B、 C、 D、6. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )A、 B、 C、 D、7. 如图,直线 , 的平分线交于点 , , 则等于( )
 A、 B、 C、 D、8. 如图,在中, , 是中线,是角平分线,是高,则下列说法中错误的是( )
A、 B、 C、 D、8. 如图,在中, , 是中线,是角平分线,是高,则下列说法中错误的是( ) A、 B、 C、 D、9. 若关于的不等式的解集为 , 则关于的不等式的解集是( )A、 B、 C、 D、10. 在锐角三角形中,是边上的高,分别以、为一边,向外作正方形和正方形 , 连接、和 , 与的延长线交于点 , 下列结论:;;;是的中线,其中结论正确的是( )
A、 B、 C、 D、9. 若关于的不等式的解集为 , 则关于的不等式的解集是( )A、 B、 C、 D、10. 在锐角三角形中,是边上的高,分别以、为一边,向外作正方形和正方形 , 连接、和 , 与的延长线交于点 , 下列结论:;;;是的中线,其中结论正确的是( )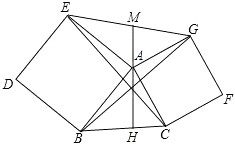 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共30.0分)
-
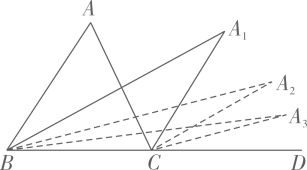
11. 命题“内错角相等”是命题.12. 已知 , 则 .13. , 是平面直角坐标系中的两点,线段的最小值为 .14. 不等式的最小整数解是 .15. 为了解海安市某校名中学生喜爱冬奥会吉祥物冰墩墩和雪容融情况,随机抽取名学生,其中有位学生喜欢冰墩墩,根据所学的统计知识可以估计该校喜欢冰墩墩的学生大约有名.16. 若 , , 则 .17. 如图,和分别是的内角平分线和外角平分线,是的平分线,是的平分线,是的平分线,是的平分线若 , 则 .
 18. 已知非负实数、、满足条件: , , 设的最大值为 , 最小值为 , 则等于 .
18. 已知非负实数、、满足条件: , , 设的最大值为 , 最小值为 , 则等于 .三、解答题(本大题共8小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:(1)、解方程组:;(2)、解不等式组: .20. 如图,将向右平移个单位,再向下平移个单位得到 .
 (1)、请你在网格图中画出的对应点分别是 , , ;(2)、直接写出平移后的点 , , 的坐标;(3)、对于内部任意一点 , 直接写出该点经过平移后对应点的坐标是 .21. 为了更好的了解青少年使用电子产品的情况,广陵区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图 , 图的统计图已知“查资料”的人数是人.
(1)、请你在网格图中画出的对应点分别是 , , ;(2)、直接写出平移后的点 , , 的坐标;(3)、对于内部任意一点 , 直接写出该点经过平移后对应点的坐标是 .21. 为了更好的了解青少年使用电子产品的情况,广陵区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图 , 图的统计图已知“查资料”的人数是人.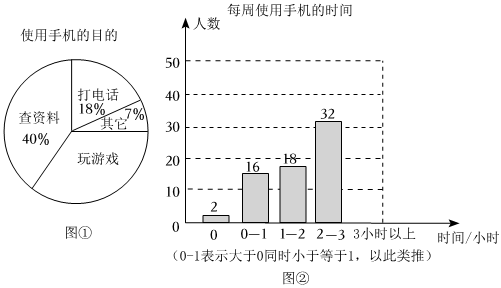 (1)、在这次调查的样本容量是;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是度;(3)、补全条形统计图;(4)、该校共有学生人,请估计每周使用手机时间在小时以上不含2小时的人数.22. 如图, 平分 , 为 延长线上一点, 交 于点 , , ,求 的度数.
(1)、在这次调查的样本容量是;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是度;(3)、补全条形统计图;(4)、该校共有学生人,请估计每周使用手机时间在小时以上不含2小时的人数.22. 如图, 平分 , 为 延长线上一点, 交 于点 , , ,求 的度数.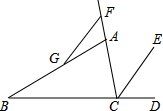 23. 如图,已知点在第一象限的角平分线上,一直角顶点与点重合,角的两边与轴、轴分别交于点,点,则:
23. 如图,已知点在第一象限的角平分线上,一直角顶点与点重合,角的两边与轴、轴分别交于点,点,则: (1)、点的坐标为多少?(2)、的值为多少?24. 某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克元;乙种蔬菜进价每千克元,售价每千克元.(1)、该超市购进甲种蔬菜千克和乙种蔬菜千克需要元;购进甲种蔬菜千克和乙种蔬菜千克需要元,求 , 的值.(2)、该超市决定每天购进甲、乙两种蔬菜共千克,且投入资金不少于元又不多于元,设购买甲种蔬菜千克正整数 , 求有哪几种购买方案.25. 已知: , 、是上的点,、是上的点, .
(1)、点的坐标为多少?(2)、的值为多少?24. 某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克元;乙种蔬菜进价每千克元,售价每千克元.(1)、该超市购进甲种蔬菜千克和乙种蔬菜千克需要元;购进甲种蔬菜千克和乙种蔬菜千克需要元,求 , 的值.(2)、该超市决定每天购进甲、乙两种蔬菜共千克,且投入资金不少于元又不多于元,设购买甲种蔬菜千克正整数 , 求有哪几种购买方案.25. 已知: , 、是上的点,、是上的点, .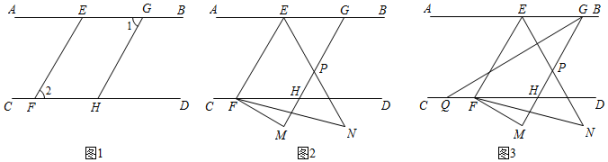 (1)、如图 , 求证:;(2)、如图 , 过点作交延长线于点 , 作、的角平分线交于点 , 交于点 , 求证:;(3)、如图 , 在(2)的条件下,作的角平分线交于点 , 若 , 直接写出的值.26. 在平面直角坐标系中,点 , , 若 , 则称点与点互为“对角点”,例如:点 , 点 , 因为 , 所以点与点互为“对角点”.
(1)、如图 , 求证:;(2)、如图 , 过点作交延长线于点 , 作、的角平分线交于点 , 交于点 , 求证:;(3)、如图 , 在(2)的条件下,作的角平分线交于点 , 若 , 直接写出的值.26. 在平面直角坐标系中,点 , , 若 , 则称点与点互为“对角点”,例如:点 , 点 , 因为 , 所以点与点互为“对角点”.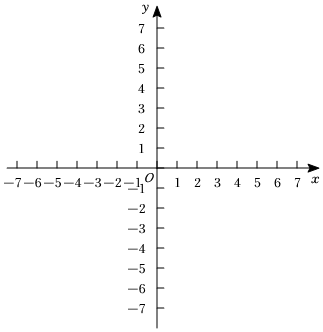 (1)、若点的坐标是 , 则在点 , , 中,点的“对角点”为点;(2)、若点的坐标是的“对角点”在坐标轴上,求点的坐标;(3)、若点的坐标是与点互为“对角点”,且点在第四象限,求 , 的取值范围.
(1)、若点的坐标是 , 则在点 , , 中,点的“对角点”为点;(2)、若点的坐标是的“对角点”在坐标轴上,求点的坐标;(3)、若点的坐标是与点互为“对角点”,且点在第四象限,求 , 的取值范围.