河南省平顶山市叶县2022-2023学年七年级下数学期末试卷

试卷更新日期：2023-07-25 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. “嫦娥”奔月、“祝融”探火、“羲和”逐日、“天和”遨游星辰 $\dots$ 在浩瀚的宇宙中谱写着中华民族飞天梦想的乐章 $.$ 下列航天图标 $($ 不考虑字符与颜色 $)$ 为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 古语有云：“水滴石穿”，若水珠不断滴在一块石头上，经过 $40$ 年，石头上会形成一个深为 $0.0000052 c m$ 的小洞 $.$ 数 $0.0000052$ 用科学记数法表示为（）

A、 $5.2 \times 1 0^{5}$ B、 $5.2 \times 1 0^{- 6}$ C、 $5.2 \times 1 0^{- 7}$ D、 $52 \times 1 0^{- 7}$

查看试题解析
3. 如图，CD⊥AB于点D，已知∠ABC是钝角，则（）

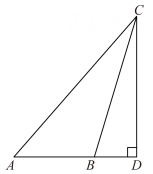A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线

查看试题解析
4. 下列计算正确的是（）

A、 $a^{5} \cdot a^{2} = a^{10}$ B、 $(a^{3})^{2} = a^{6}$ C、 $(a b^{3})^{2} = a b^{6}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
5. 用两个完全一样的含30°角的三角尺画平行线，下列画出的直线a与b不一定平行的是（）

A、 B、 C、 D、

查看试题解析
6. 对于两个事件：
事件 $1$ ：任意掷一枚质地均匀的正方体骰子，掷出的点数是小于 $6$ ；
事件 $2$ ：口袋中有除颜色外其他都完全相同的 $2$ 个红球和 $1$ 个白球，从中摸出 $2$ 个球，其中至少一个是红球：
有如下说法，其中正确的是（）

A、事件 $1$ 、 $2$ 均为必然事件 B、事件 $1$ 、 $2$ 均为随机事件 C、事件 $1$ 是随机事件，事件 $2$ 是必然事件 D、事件 $1$ 是必然事件，事件 $2$ 是随机事件

查看试题解析
7. 下列判断中，正确的是（）

A、直角三角形一定不是轴对称图形 B、角是轴对称图形，角平分线是它的对称轴 C、线段是轴对称图形，它的对称轴是过该线段中点的任意一条直线 D、等边三角形是轴对称图形，它有三条对称轴

查看试题解析
8. 如图， $E$ 是直线 $C A$ 上一点， $∠ F E A = 40 °$ ，射线 $E B$ 平分 $∠ C E F$ ， $G E ⊥ E F$ ，则 $∠ G E B$ 的度数为（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
9. 乐乐所在的七年级某班学生到野外活动，为测量池塘两端 $A$ ， $B$ 的距离，乐乐、明明、聪聪三位同学分别设计出如下几种方案：
乐乐：如图 $①$ ，先在平地取一个可直接到达 $A$ ， $B$ 的点 $C$ ，再连接 $A C$ ， $B C$ ，并分别延长 $A C$ 至 $D$ ， $B C$ 至 $E$ ，使 $D C = A C$ ， $E C = B C$ ，最后测出 $D E$ 的长即为 $A$ ， $B$ 的距离．
明明：如图 $②$ ，先过点 $B$ 作 $A B$ 的垂线 $B F$ ，再在 $B F$ 上取 $C$ ， $D$ 两点，使 $B C = C D$ ，接着过点 $D$ 作 $B D$ 的垂线 $D E$ ，交 $A C$ 的延长线于点 $E$ ，则测出 $D E$ 的长即为 $A$ ， $B$ 的距离．
聪聪：如图 $③$ ，过点 $B$ 作 $B D ⊥ A B$ ，再由点 $D$ 观测，在 $A B$ 的延长线上取一点 $C$ ，使 $∠ B D C = ∠ B D A .$ 这时只要测出 $B C$ 的长即为 $A$ ， $B$ 的距离．
以上三位同学所设计的方案中可行的是（）

A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行

查看试题解析
10. 放学后，小刚和同学边聊边往家走，突然想起今天是妈妈的生日，赶紧加快速度，跑步回家．小刚离家的距离 $s ($ 单位 $m)$ 和放学后的时间 $t ($ 单位 $m i n)$ 之间的关系如图所示，那么下列说法错误的是（）

A、小刚边走边聊阶段的行走速度是 $125 m / m i n$ B、小刚家离学校的距离是 $1000 m$ C、小刚回到家时已放学 $10 m i n$ D、小刚从学校回到家的平均速度是 $100 m / m i n$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

11. 已知 $a^{m} = 3$ ， $a^{n} = 6$ ，则 $a^{m - n} =$ ．

查看试题解析

12. 为了解某品牌汽车的耗油量，人们对这种车在高速公路上做了耗油试验，并把试验的数据记下来，制成下表：

汽车行驶时间 $t (h)$	$0$	$1$	$2$	$3$	$\dots$
邮箱剩余油量 $Q (L)$	$100$	$94$	$88$	$82$	$\dots$

根据上表的数据，写出 $Q$ 与 $t$ 的关系式：．

查看试题解析

13. 如图是 $3 \times 3$ 的正方形网格，要在图中再涂黑一个小正方形，使得图中黑色的部分成为轴对称图形，这样的小正方形有个．

查看试题解析
14. 如图，小虎用 $10$ 块高度都是 $3 c m$ 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板 $(A C = B C ， ∠ A C B = 90 °)$ ，点 $C$ 在 $D E$ 上，点 $A$ 和 $B$ 分别与木墙的顶端重合，则两堵木墙之间的距离为 $c m$ ．

查看试题解析
15. 如图， $A B / / C D$ ， $∠ B E D = 110 °$ ， $B F$ 平分 $∠ A B E$ ， $D F$ 平分 $∠ C D E$ ，则 $∠ B F D =$ ．

查看试题解析

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）

16. 计算及化简求值．

(1)、 $(2023 - π)^{0} - 3^{2} + (\frac{1}{2})^{- 3}$ ；

(2)、 $m^{2} \cdot m^{6} - (2 m^{2)^{4}} + m^{9} \div m$ ；

(3)、先化简，再求值； $x (x - 4 y) + (2 x + y) (2 x - y) - (2 x - y)^{2}$ ，其中 $x = - 2 ， y = - \frac{1}{2}$ ．

查看试题解析
17. 请在网格中完成下列问题：

(1)、在图 $1$ 中画出 $△ A B C$ 关于直线 $P Q$ 成轴对称的 $△ A' B' C'$ ；

(2)、在图 $2$ 中画出 $△ A B C$ 与 $△ D E F$ 的对称轴．

查看试题解析
18. 甲袋中有红球8个、白球5个和黑球12个；乙袋中有红球18个、白球9个和黑球23个．（每个球除颜色外都相同）

(1)、若从中任意摸出一个球是红球，选哪袋成功的机会大？请说明理由；

(2)、“从乙袋中取出10个红球后，乙袋中的红球个数和甲袋中红球个数一样多，所以此时若从中任意摸出一个球是红球，选甲、乙两袋成功的机会相同”．你认为这种说法正确吗？为什么？

查看试题解析
19. 一直以来，人们力图探寻地球内部的奥秘，科学家做了大量的模拟实验后发现：地表以下岩层的温度 $y (℃)$ 随着所处深度 $x (k m)$ 的变化而变化，在某个地点 $y$ 与 $x$ 之间的关系可近似地表示为 $y = 35 x + 20$ ．

(1)、根据关系式，下表列出部分因变量 $y$ 与自变量 $x$ 的对应值，请补充表中所缺的数据；
所处深度 $x (k m)$
2
3
4
5
6
7
          $\dots$
岩层的温度 $y (℃)$
90
125
195
265
          $\dots$

(2)、当所处深度 $x (k m)$ 每增加 $1 k m$ ，岩层的温度 $y (℃)$ 是怎样变化的？

(3)、当岩层的温度 $y (℃)$ 达到 $1000 ℃$ 时，根据上述关系式，求所处的深度．

查看试题解析
20. 如图，若 $∠ B + ∠ B C D = 180 °$ ， $∠ B = ∠ D$ ，则 $∠ E = ∠ D F E .$ 为什么？
请在下面的括号里填写理由：
因为 $∠ B + ∠ B C D = 180 ° ($ 已知 $)$ ，
所以 $A B / / C D$ （  ）.
所以 $∠ B = ∠ D C E$ （  ）.
又因为 $∠ B = ∠ D$ （已知），
所以 $∠ D = ∠ D C E$ （等量代换）．
所以 $A D / / B E$ （  ）.
      $∠ E = ∠ D F E$ （  ）.

查看试题解析
21. 如图，已知点 $B$ ， $E$ ， $C$ ， $F$ 在一条直线上， $B E = C F$ ， $A C / / D E$ ， $∠ A = ∠ D$ ．

(1)、求证： $△ A B C$ ≌ $△ D F E$ ；

(2)、若 $B F = 20$ ， $E C = 8$ ，求 $B C$ 的长．

查看试题解析
22. 乘法公式的探究及应用．

(1)、，阴影部分的面积可表示为； $($ 用含字母 $a$ ， $b$ 的式子表示 $)$

(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是 $. ($ 均用含字母 $a$ ， $b$ 的代数式表示 $)$

(3)、比较左、右两图的阴影部分面积，可以得到乘法公式； $($ 用式子表达 $)$

(4)、运用你所得到的公式，计算下列各题：
① $202 2^{2} - 2021 \times 2023$ ；
② $(2 m + n + p) (2 m + n - p)$ ．

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是直线 $B C$ 上一点，连接 $A D$ ，以 $A D$ 为边向右作 $△ A D E$ ，使得 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接 $C E$ ．

(1)、如图 $1$ ，当点 $D$ 在 $B C$ 边上时，
①若 $∠ B A C = 40 °$ 时，则 $∠ D C E =$ ▲ $°$ ；
②若 $∠ B A C = 80 °$ 时，则 $∠ D C E =$ ▲ $°$ ；
③观察以上结果，猜想 $∠ B A C$ 与 $∠ D C E$ 的数量关系，并说明理由．

(2)、当点 $D$ 在 $B C$ 的延长线上时，请判断 $∠ B A C$ 与 $∠ D C E$ 的数量关系，并说明理由．

查看试题解析

所处深度 $x (k m)$	2	3	4	5	6	7	$\dots$
岩层的温度 $y (℃)$	90	125		195		265	$\dots$