2023-2024学年北师大版数学七年级上册3.5探究与表达规律(复习卷)
试卷更新日期:2023-07-24 类型:同步测试
一、选择题
-
1. 如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )
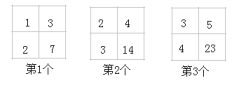 A、62 B、79 C、88 D、982. 如图所示的运算程序中,若开始输入的x的值为 , 我们发现第1次输出的结果为 , 第2次输出的结果为 , …,第2023次输出的结果为( )
A、62 B、79 C、88 D、982. 如图所示的运算程序中,若开始输入的x的值为 , 我们发现第1次输出的结果为 , 第2次输出的结果为 , …,第2023次输出的结果为( )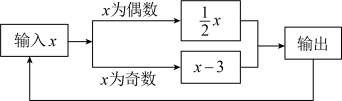 A、 B、 C、 D、3. 1883年,康托尔用以下的方法构造的这个分形,称做康托尔集.如图,取一条长度为1的线段,将它三等分,去掉中间一段,留剩下两段,这称为第一阶段;然后将剩下的两段再三等分,各去掉中间一段,剩下更短的四段,这称为第二阶段…将这样的操作无限地重复下去,余下的无穷点就称做康托尔集.那么经过第四个阶段后,留下的线段的长度之和为( )
A、 B、 C、 D、3. 1883年,康托尔用以下的方法构造的这个分形,称做康托尔集.如图,取一条长度为1的线段,将它三等分,去掉中间一段,留剩下两段,这称为第一阶段;然后将剩下的两段再三等分,各去掉中间一段,剩下更短的四段,这称为第二阶段…将这样的操作无限地重复下去,余下的无穷点就称做康托尔集.那么经过第四个阶段后,留下的线段的长度之和为( ) A、 B、 C、 D、4. 已知整数……满足下列条件: , , , ……依次类推,则的值为( )A、 B、 C、 D、5. 正整数按如图所示的规律排列,则第9行、第列的数字是( )
A、 B、 C、 D、4. 已知整数……满足下列条件: , , , ……依次类推,则的值为( )A、 B、 C、 D、5. 正整数按如图所示的规律排列,则第9行、第列的数字是( ) A、 B、 C、 D、6. 有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )
A、 B、 C、 D、6. 有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )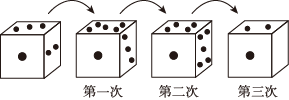 A、5 B、3 C、4 D、27. 按如图所示的运算程序,若开始输入x的值为343,则第2022次输出的结果为( )
A、5 B、3 C、4 D、27. 按如图所示的运算程序,若开始输入x的值为343,则第2022次输出的结果为( ) A、343 B、1 C、7 D、498. 将一列有理数 , ……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(的位置)是有理数4,那么,“峰6”中的位置是有理数____,2022应排在、、、、中____的位置.正确的选项是( )
A、343 B、1 C、7 D、498. 将一列有理数 , ……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(的位置)是有理数4,那么,“峰6”中的位置是有理数____,2022应排在、、、、中____的位置.正确的选项是( )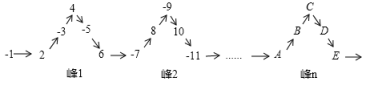 A、-29, B、30, C、029, D、-31,9. 下图是一组有规律的图案,它们是由边长相同的黑白两种颜色的小正方形组成的.按照这样的规律,第505个图案中有黑色小正方形( )
A、-29, B、30, C、029, D、-31,9. 下图是一组有规律的图案,它们是由边长相同的黑白两种颜色的小正方形组成的.按照这样的规律,第505个图案中有黑色小正方形( )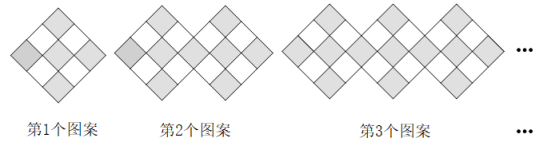 A、2021个 B、2022个 C、2023个 D、2024个10. 定义一种对正整数的“”运算:①当为奇数时,;②当为偶数时,(其中,是使为奇数的正整数), , 两种运算交替重复进行,例如,取 , 则运算过程如图所示:若 , 则第2023次“”运算的结果是( )
A、2021个 B、2022个 C、2023个 D、2024个10. 定义一种对正整数的“”运算:①当为奇数时,;②当为偶数时,(其中,是使为奇数的正整数), , 两种运算交替重复进行,例如,取 , 则运算过程如图所示:若 , 则第2023次“”运算的结果是( ) A、3 B、9 C、18 D、48
A、3 B、9 C、18 D、48二、填空题
-
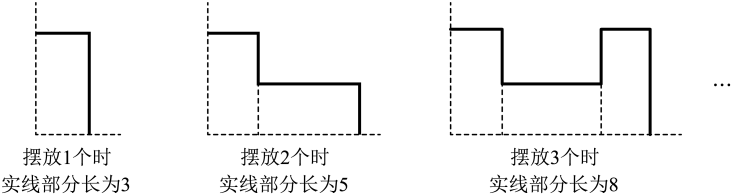
11. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.
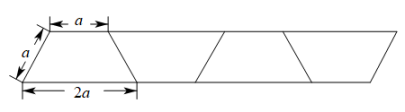
 12. 观察图形并填表(单位:)
12. 观察图形并填表(单位:)梯形个数
1
2
3
4
5
6
…
n
图形周长
…
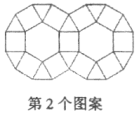
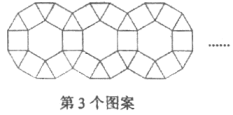
 13. 如图,观察下列的“蜂窝图”,则第n个图案中的正六边形的个数是(用含n的代数式表示).
13. 如图,观察下列的“蜂窝图”,则第n个图案中的正六边形的个数是(用含n的代数式表示).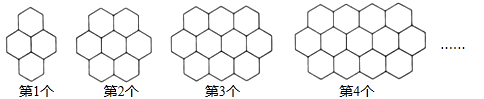 14. 如图是用正三角形、正方形、正六边形设计的一组图案,按照规律,第个图案中正三角形的个数是.
14. 如图是用正三角形、正方形、正六边形设计的一组图案,按照规律,第个图案中正三角形的个数是.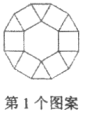
 15. 如图是用棋子摆成的图形,按照这种摆法,第个图形中共有个棋子.
15. 如图是用棋子摆成的图形,按照这种摆法,第个图形中共有个棋子.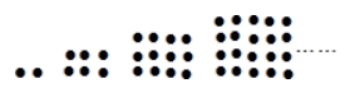
三、解答题
-
16. 我校七年级数学兴趣小组成员们自主开展数学微项目研究.结合本阶段学内容特点,他们决定研究数的一些“神秘”性质.
探索数的神秘性质
素材
尼科马霍斯是古希腊数学家,他的著作算术入门中记载了各种数分门别类的整理成果,其中任何一个整数的立方都可以写成个连续奇数之和.
举例论证:
;;;
请你按规律写出:
▲ .
规律总结
当是奇数7时,则等号右边式子中的中间数即第4个数为 ▲ ;
当为偶数10时,则等号右边式子中的中间两个数即第5和第6个数为 ▲ .
综合应用
利用上面结论计算:.
拓展延伸
我们还发现以下规律:已知 , , 且 , 均为正整数,如果将进行如图所示的“分解”:
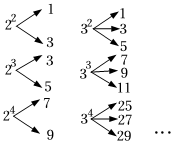
若且 , 均为不大于的正整数的分解中有奇数31,则的值为 ▲ .
17. 观察下列三行数并按规律填空:-1,2,-3,4,-5, ▲ , ▲ , …;
1,4,9,16,25, ▲ , ▲ , …;
0,3,8,15,24, ▲ , ▲ , ….
( 1 )第一行数按什么规律排列?
( 2 )第二行数、第三行数分别与第一行数有什么关系?
( 3 )取每行数的第10个数,计算这三个数的和.
18. 图1中,有一个平行四边形;图2中,由2个相同的平行四边形拼成一排的图形,这图形中可以找到3个平行四边形;
图3中,由3个相同的平行四边形拼成一排的图形,这图形中可以找到6个平行四边形;

由此我们可以提出一个这样的问题:
图4中,由4个相同的平行四边形拼成一排的图形中,可以找到几个平行四边形?
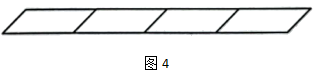
答:10个
请你根据以上事实,将一些相同的平行四边形横向或纵向拼接,由此提出一个数学问题,并写出答案.
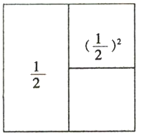 ⇒ +( )2=1﹣( )2;
⇒ +( )2=1﹣( )2;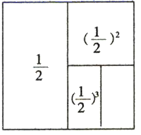 ⇒ +( )2+( )3=
⇒ +( )2+( )3=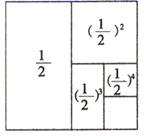 ⇒ +( )2+( )3+( )4=
⇒ +( )2+( )3+( )4=