2023-2024学年北师大版数学七年级上册3.4整式的加减（培优卷）

试卷更新日期：2023-07-24 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形，并将①号、②号、③号正方形按图2方式叠放入④号正方形内部，若需求出阴影部分的周长和，只需知道下列哪个正方形的边长（）

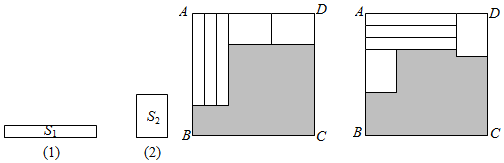
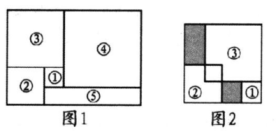A、①号 B、②号 C、③号 D、④号

查看试题解析
2. 如图，用三个同图①的长方形和两个同图②的长方形用两种方式去覆盖一个大的长方形ABCD，两种方式未覆盖的部分(阴影部分)的周长相等，那么图①中长方形的面积S₁与图②中长方形的面积S₂的比是（）

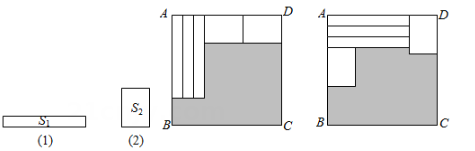A、2：3 B、1：2 C、3：4 D、1：1

查看试题解析
3. 把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m，宽为n内(如图②)，大长方形未被卡片覆盖的部分用阴影表示.当m不变，n变长时，阴影部分的面积差总保持不变，则a，b应满足的关系为（ )

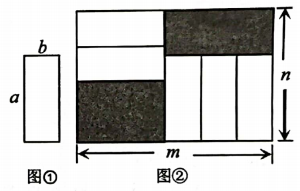A、a=5b B、a=3b C、a=2b D、 $a = \frac{3}{2} b$

查看试题解析
4. 如图，将图1中的长方形纸片前成（1）号、（2）号、（3）号、（4）号正方形和（5）号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）

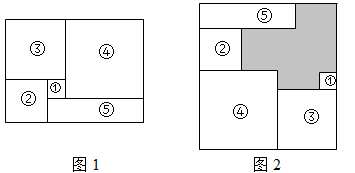A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道（3）号正方形的周长即可 D、只需知道（5）号长方形的周长即可

查看试题解析
5. 图1是长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 $A B C D$ 内，已知 $C D$ 的长度固定不变， $B C$ 的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为 $S_{1}$ ， $S_{2}$ ，若 $S = S_{1} - S_{2}$ ，且 $S$ 为定值，则 $a$ ， $b$ 满足的关系是（）

A、 $a = 2 b$ B、 $a = 3 b$ C、 $a = 4 b$ D、 $a = 5 b$

查看试题解析
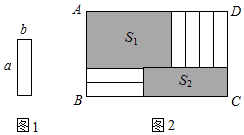6. 将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（）

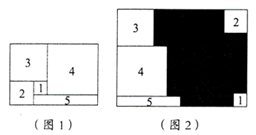A、16 B、24 C、30 D、40

查看试题解析
7. 如图，在一个长方形中放入三个正方形，从大到小正方形的边长分别为 $a$ 、 $b$ 、 $c$ ，则右上角阴影部分的周长与左下角阴影部分周长差为（）

A、a+b B、 $b + c$ C、 $2 a$ D、 $2 b$

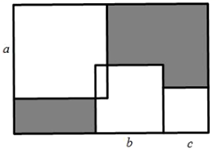查看试题解析
8. 如果 $a 、 b 、 c 、 d$ 为互不相等的有理数，且 $| a - c | = | b - c | = | d - b | = 2$ ，那么 $| a - d | =$ （）

A、8 B、6 C、4 D、2

查看试题解析
9. 已知代数式x²＋ax－2y＋7－(bx²－2x＋9y－1)的值与x的取值无关，则a＋b的值为（）

A、－1 B、1 C、－2 D、2

查看试题解析
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm，宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）

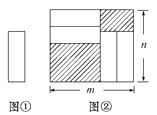A、4mcm B、4ncm C、2(m+n)cm D、4(m-n)cm

查看试题解析

二、填空题

11. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“英华数”，定义新运算：将一个“英华数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω （ 27 ）$ ．

(2)、若m，n都是“英华数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析
12. 如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形 $A B C D$ ，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积 $S_{1}$ 与（2）图长方形的面积 $S_{2}$ 的比是.

查看试题解析
13. 点 $A$ 、 $B$ 在数轴上分别表示有理数 $a$ 、 $b$ ，则在数轴上 $A$ 、 $B$ 两点之间的距离为 $A B = | a - b |$ ，利用数轴上两点间距离，可以得到 $| x + 1 | - | x - 3 |$ 的最大值是．

查看试题解析
14. 已知 $a < - 1$ ， $- 1 \leq c \leq 0$ ， $a < b < c$ ，则 $| a + b + c | - | b - c | - | a - c - 1 |$ 的最小值为，最大值为.

查看试题解析
15. 有一道题目是一个多项式减去x²＋14x－6，小强误当成了加法计算，结果得到2x²－x＋3，则原来的多项式是．

查看试题解析

三、解答题

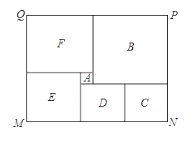
16. 如图，它是由A、B、E、F四个正方形，C、D两个长方形拼成的大长方形，已知正方形F的边长为6，求拼成的大长方形周长．

查看试题解析
17. 小亮在计算一个多项式与 $3 x^{2} - 2 x + 7$ 的差时，因误以为是加上 $3 x^{2} - 2 x + 7$ 而得到答案 $5 x^{2} + 2 x + 4$ ，请求出这个问题的正确答案.

查看试题解析
18. 已知A=a²-2ab+b² ， B=-a²-3ab-b²,求：2A-3B。

查看试题解析
19. 综合与探究
如图，数轴上有一点 $O$ 从原点开始出发，先向左移动 $3 c m$ （1个单位长度表示 $1 c m$ ）到达 $A$ 点，再向左移动 $2 c m$ 到达 $B$ 点，然后向右移动 $8 c m$ 到达 $C$ 点．

(1)、请在题中所给的数轴上表示出 $A$ ， $B$ ， $C$ 三点的位置．

(2)、把点 $C$ 到点 $A$ 的距离记为 $C A$ ，则 $C A =$ cm；若数轴上的点 $M$ 表示的数为 $x$ ，点 $N$ 表示的数为 $y (x < y)$ ，则 $M N =$ cm．

(3)、若点 $B$ 以每秒 $2 c m$ 的速度向左移动，同时点 $A$ ， $C$ 分别以每秒 $3 c m$ 、 $8 c m$ 的速度向右移动，设移动时间为 $t (t > 0)$ 秒，试探究 $C A - A B$ 的值是否会随着 $t$ 的变化而变化，请说明理由．

查看试题解析

20. 某市居民使用自来水按如下标准收费（水费按月缴纳）

居民月用水量

不超过 $10 m^{3}$ 的部分

超过 $10 m^{3}$ 但

不超过 $20 m^{3}$ 的部分

超过 $20 m^{3}$ 的部分

单价

2元 $/ m^{3}$

3元 $/ m^{3}$

4元 $/ m^{3}$

(1)、某用户一个月用了

16 m^{3}

水，求该用户这个月应缴纳的水费；

(2)、设某户月用水量为

n

立方米，当

n > 20

时，求该用户应缴纳的水费（用含

n

的代数式表示）；

(3)、甲、乙两用户一个月共用水

40 m^{3} .

已知甲用户缴纳的水费超过了20元，设甲用户用水

x m^{3}

，则甲、乙两用户一个月共缴纳水费多少元？（用含

x

的代数式表示）

查看试题解析