2023-2024学年北师大版数学七年级上册3.2代数式(提升卷)
试卷更新日期:2023-07-24 类型:同步测试
一、选择题
-
1. 已知 , 则代数式的值是( )A、-3 B、-1 C、2 D、32. 【阅读理解】计算:25×11=275,13×11=143,48×11=528,74×11=814,观察算式,我们发现两位乘11的速算方法:头尾一拉,中间相加,满十进一.
【拓展应用】已知一个两位数,十位上的数字是a,个位上的数字是b,这个两位数乘11,计算结果的十位上的数字可表示为( )
A、a或a+1 B、a+b或ab C、a+b−10 D、a+b或a+b−103. 已知 , , 则的值为( )A、 B、2 C、14 D、164. 已知 , 则代数式的值为( )A、2023 B、-2021 C、2021 D、-20235. 如图是同一时刻北京时间和莫斯科时间.若现在北京时间是x,则同一时刻莫斯科的时间可以表示为( ) A、 B、 C、 D、6. 已知x+2y=7,4m-3n=8,则代数式(9n-4y)-2(6m+x)+3的值为( )A、38 B、35 C、-35 D、-327. 若代数式的值为2,则代数式的值为A、6 B、-6 C、8 D、-108. 按下面的运算程序计算:
A、 B、 C、 D、6. 已知x+2y=7,4m-3n=8,则代数式(9n-4y)-2(6m+x)+3的值为( )A、38 B、35 C、-35 D、-327. 若代数式的值为2,则代数式的值为A、6 B、-6 C、8 D、-108. 按下面的运算程序计算:
当输入时,输出结果为33;当输入时,输出结果为17.如果输入n的值为正整数 , 输出的结果为25,那么满足条件的n的值最多有( )
A、1个 B、2个 C、3个 D、4个9. 若2a2+b=4,则代数式3-4a2-2b的值为( )A、11 B、7 C、-1 D、-510. 当时,代数式的值为 , 则时,代数式的值为( )A、 B、 C、 D、二、填空题
-
11. 若的值为5,则的值为.12. 历史上数学家欧拉最先把关于x的多项式用记号来表示,把x等于某数a时的多项式的值用来表示.例如,对于多项式 , 当时,多项式的值为.若对于多项式 , 有 , 则的值为.13. 已知 , 则.14. 按如图所示程序运算,x为不超过20的自然数.当输入值x为时,输出值最小.
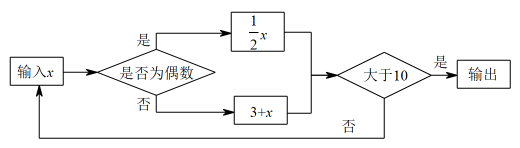 15. 若 , 则的值为.
15. 若 , 则的值为.三、解答题