吉林省吉林市永吉县2022-2023学年八年级下学期期末考试数学试题

试卷更新日期：2023-07-24 类型：期末考试

进入出卷网下载

一、单项选择题（每小题2分，共12分）

1. 若式子 $\sqrt{2 x - 6}$ 有意义，则实数x的取值范围是（　　）

A、x＞3 B、x＜3 C、x≤3 D、x≥3

查看试题解析
2. 下列各式计算正确的是（　　）

A、 $\sqrt{27} \div \sqrt{3} = 3$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $5 \sqrt{2} - 4 \sqrt{2} = 1$ D、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$

查看试题解析
3. 直角三角形的一条直角边和斜边分别为3和5，则其面积为（　　）

A、7.5 B、7 C、6 D、4

查看试题解析
4. 将函数y=-3x的图象沿y轴向上平移2个单位长度后，得到图象的对应函数解析式
为（　　）

A、 $y = - 3 (x - 2)$ B、 $y = - 3 x + 2$ C、 $y = - 3 x - 2$ D、 $y = - 3 (x + 2)$

查看试题解析
5. 如图，在正方形ABCD中，对角线AC的长为4，则正方形ABCD的面积为（　　）

A、4 B、8 C、12 D、16

查看试题解析
6. “漏壶”是一种古代计时器．在它内部盛一定量的水，水从壶下的小孔漏出．壶内壁有刻度，人们根据壶中水面的位置计算时间．用x表示时间，y表示壶底到水面的高度．
（不考虑水量变化对压力的影响）下面图象适合表示y与x的对应关系的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题（每小题3分，共24分）

7. 计算： $\sqrt{{(- 4)}^{2}}$ = ．

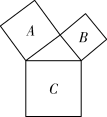
查看试题解析
8. 若关于x的一元二次方程 $x^{2} + 6 x + m = 0$ 有两个相等的实数根，则m的值为．

查看试题解析
9. 如图，图中的三角形为直角三角形，已知正方形A和正方形B的面积分别为25和9，则正方形C的面积为．

查看试题解析
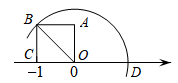
10. 如图，在数轴上，以1个单位长度为边长作正方形OABC，以数轴的原点O为圆心，
正方形的对角线OB为半径画弧，交数轴的正半轴于点D，则点D所表示的数为．

查看试题解析
11. 如图，矩形ABCD的对角线AC，BD相交于O，若E，F分别为OA，AD的中点，并且AC=8 cm，则EF的长为cm．

查看试题解析
12. 如图，菱形ABCD的周长为24，点A的坐标为（ $2 \sqrt{5}$ ， 0），则点D的坐标为．

查看试题解析
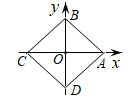13. 下表记录了甲、乙、丙、丁四名运动员跳远选拔成绩（单位：cm）的平均数和方差，要从中选择一名成绩较高且发挥稳定的远动员参加决赛，最合适的远动员是．

甲
乙
丙
丁
平均数
380
360
380
350
方差
12.5
13.5
2.4
2.7

查看试题解析
14. 如图，在平面直角坐标系中，点A的坐标为（3，0），点B在y轴上，AB=5，将△OAB沿x轴向右平移，当点B落在直线y=2x-8上时，线段AB扫过的面积为．

查看试题解析

三、解答题（每小题5分，共20分）

15. 解方程： $3 x_{}^{2} + 12 x = 0$ ．

查看试题解析
16. 计算： $\sqrt{5} - \sqrt{20} + \sqrt{90} \div \sqrt{2}$ ．

查看试题解析
17. 若实数a，b，c满足： $| a - \sqrt{7} | + \sqrt{b - 5} + (c - 4 \sqrt{2})_{}^{2} = 0$ ．

(1)、a= ， b= ， c= ．

(2)、以a，b，c长为边能否构成三角形？若能，能够成什么形状的三角形？（直接回答，不用说明理由）

查看试题解析
18. 如图，在平面直角坐标系中，直线 $y = - \frac{1}{2} x - 1$ 与直线 $- 2 x + 2$ 相交于点P．

(1)、求点P的坐标．

(2)、直接写出：不等式 $- 2 x + 2 > - \frac{1}{2} x - 1$ 的解集．

查看试题解析

四、解答题（每小题7分，满分28分）

19. 如图，菱形ABCD的周长为200 cm，对角线AC，BD相交于O，并且AC=60 cm．

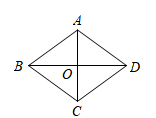(1)、①AB= ▲ cm，OA= ▲ cm；
②求对角线BD的长．

(2)、菱形ABCD的面积为cm² ．

查看试题解析
20. 图1，图2，图3是三张形状、大小完全相同的6×6方格纸，每个小正方形的顶点称为格点，每个小正方形的边长均为1．线段AB的两个端点A，B都在格点上．

(1)、在图1中画出一个以点A，B为顶点的平行四边形，且面积为16（要求所作的平行四边形的各个顶点都在格点上）．

(2)、在图2中画出一个以点A，B为顶点的矩形，且面积为4（要求所作的矩形的各个顶点都在格点上）．

(3)、在图3中画出一个以点A，B为顶点的菱形，且面积为8（要求所作的菱形的各个顶点都在格点上）．

查看试题解析
21. 已知张强家、体育场、文具店在同一条直线上．下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中x表示时间，y表示张强离家的距离．

根据图象回答下列问题：

(1)、体育场离张强家km，张强从家到体育场用了min；

(2)、体育场离文具店km；

(3)、张强在体育场锻炼了min，在文具店停留了min；

(4)、求张强从文具店回家的平均速度是多少？

查看试题解析
22. 如图，在 $▱ABCD$ 中，对角线AC和BD相交于点O，并且OA=OD．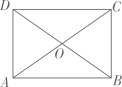

(1)、求证：四边形ABCD是矩形；

(2)、若∠OBC=55°，则∠AOB的度数为．

查看试题解析

五、解答题（每小题8分，共16分）

23. 某校240名学生参加植树活动，要求每人植树4~7棵，活动结束后随机抽查了20名
学生每人的植树量，并分为四类：A类4棵、B类5棵、C类6棵、D类7棵，将各类人数绘制成如图所示的不完整的条形统计图，回答下列问题：

(1)、补全条形统计图．

(2)、直接写出这20名学生每人植树量的众数和中位数．

(3)、估计这240名学生共植树多少棵？

查看试题解析
24. 如图，直线l₁： $y = x + b$ 与x轴相交于点A，直线l₂： $y = - \frac{2}{3} x + \frac{4}{3}$ 与x轴相交于点B，直线l₁和l₂相交于点C（m，2）．

(1)、求b的值．

(2)、求△ABC的面积．

查看试题解析

六、解答题（每小题10分，共20分）

25. 如图，矩形AEBO的对角线AB和OE相交于点F．延长AO到C，使OC=OA，延长BO到D，使OD=OB，连接AD，CD，BC．

(1)、求证：四边形BCOE是平行四边形；

(2)、求证：四边形ABCD是菱形；

(3)、若OE=10，∠BCD=60°，则菱形ABCD的面积为．

查看试题解析
26. 为了推进乡村振兴发展，某地决定对A，B两村之间的公路进行改造，并由甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工2天，乙工程队再开始施工．乙工程队施工几天后，因另有任务提前离开，余下的任务由甲工程队单独完成，直到公路修通．甲、乙两个工程队修筑公路的长度y（米）与甲工程队施工时间x（天）之间的函数关系如图所示，请根据图象提供的信息，解答下列问题：

(1)、乙工程队每天修路米，甲工程队每天修路米，a的值为， b的值为．

(2)、直接写出：甲工程队修公路的长度y（米）与甲施工队施工时间x（天）之间的函数关系式．

(3)、求乙工程队修公路的长度y（米）与甲工程队施工时间x（天）之间的函数关系式．

(4)、若该项工程由甲、乙两工程队从开始就合作施工，直到任务完成，直接写出：完成任务所需的时间．

查看试题解析

	甲	乙	丙	丁
平均数	380	360	380	350
方差	12.5	13.5	2.4	2.7