吉林省吉林市丰满区2022-2023学年八年级下学期期末考试数学试题

试卷更新日期：2023-07-24 类型：期末考试

进入 出卷网 下载

一、单项选择题(每小题2分，共12分)

  • 1.  二次根式a在实数范围内有意义，则a的取值范围是（  ）
    A、a≥0 B、a>0 C、a≤0 D、a<0

    查看试题解析

  • 2.  若一个直角三角形的两条直角边长分别是6和8，则斜边长是（  ）
    A、6 B、7 C、8 D、10

    查看试题解析

  • 3.  某次教学技能大赛，7位评委对张老师上课的评分分别为a1 ， a2 ， a3 ， a4 ， a5 ， a6 ， a7 ， 若去掉其中一个最高分和一个最低分得到一组新数据b1 ， b2 ， b3 ， b4 ， b5 ， 则这两组数据一定相同的是（  ）
    A、平均数 B、中位数 C、众数 D、方差

    查看试题解析

  • 4. 如图，在菱形ABCD中，∠B=60° ， 若对角线AC=2，则菱形ABCD的周长为（ ）

    A、2 B、4 C、6 D、8

    查看试题解析

  • 5.  如图，在ABCD中，AB=15，BC=13，过点A作AE⊥DC于点E，若AE=12，则EC的长度为（  ）

    A、8. B、9. C、10. D、12.

    查看试题解析

  • 6.  如图，四边形ABCD是矩形，对角线AC，BD相交于点O，若DE垂直平分OC，且OC=2，则DE的长度为（  ）

    A、1 B、2 C、3 D、2

    查看试题解析

二、填空题(每小题3分，共24分)

  • 7. 化简 12=   ．

    查看试题解析

  • 8.  一次函数y=2x−1的图象不经过第象限. 

    查看试题解析

  • 9.  如图，在菱形ABCD中，若∠1=28° ， 则∠D=°．

    查看试题解析

  • 10.  如图，将矩形纸片ABCD沿BM折叠，使点A刚好落在对角线BD上的点A'处，若∠DBC=30° ， 则∠A'MB=°．

    查看试题解析

  • 11.  如图，点O是数轴的原点，OA⊥OB，OA=OB=1，以A为圆心，AB为半径画弧，交数轴于点C，则点C对应的实数是 ．  

    查看试题解析

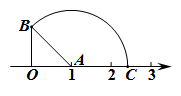  • 12. 如图，在平面直角坐标系中，Rt△AOC的斜边OA在第一象限，过点A作AB⊥x轴于点B，若AB=3，OB=4，点E为OA的中点，则CE= ．

    查看试题解析

  • 13.  如图，直线y=−43x+4与x轴，y轴分别交于点A，B两点，则原点O到直线AB的距离为 ．

    查看试题解析

  • 14.  将若干个正方形按如图所示方式放置，每个正方形有一个顶点在直线y=x+1上，两个顶点在x轴上，则点B2023的纵坐标是 ．

    查看试题解析

三、解答题(每小题5分，共20分)

  • 15.  计算：3×10÷6 ．

    查看试题解析

  • 16. 计算：18−8+2

    查看试题解析

  • 17. 已知x=5 ， y=2 ， 求(x−y)2的值．

    查看试题解析

  • 18. 我国古代数学著作《九章算术》中有这样一个问题. 有一个水池，水面是一个边长为10尺（AB=10尺）的正方形，在水池正中央有一根芦苇(点P是AB的中点)，它高出水面1尺(MP=1尺). 如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面(MN=BN). 水的深度PN与这根芦苇MN的长度分别是多少？

    查看试题解析

四、解答题(每小题7分，共28分)

  • 19.  如图，在平行四边形ABCD中，点E，F分别为AD，CD边上的点，DE=DF，

    ∠1=∠2. 

    求证：平行四边形ABCD是菱形．

    查看试题解析

  • 20.  如图，在6×6正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A，B，C都在格点上，按下列要求作图，使得所画图形的顶点均在格点上. 

    (1)、在图1中BC所在直线上方找到一个格点D，连接DB，DC，使S△DBC=S△ABC. 
    (2)、在图2中确定一点E，使四边形ABEC为正方形. 
    (3)、在图3中BC所在直线下方有个格点到BC两点距离相等. 

    查看试题解析

  • 21.  某公司欲招聘一名公关人员，对甲、乙两位应试者进行了笔试和面试，他们各自成绩(百分制)如下表所示.                                                                                                                   

    应试者

    笔试

    面试

    甲

    85

    75

    乙

    60

    95

    (1)、如果公司认为笔试和面试同等重要，从他们的成绩看，被录取的是；
    (2)、如果公司认为，作为公关人员面试应该比笔试更重要，按笔试成绩占40%，面试成绩占60%，计算应试者的平均成绩(百分制)，谁将被录取？

    查看试题解析

  • 22.  如图，在平面直角坐标系中，一次函数y=kx+1(k≠0)的图象过点A(2，0)，将图象向上平移2个单位后与x轴交于点B，与y轴交于点C，

    (1)、求k的值；
    (2)、直接写出图象经过点B和点C的一次函数的解析式为；
    (3)、请求出△OBC的面积. 

    查看试题解析

五、解答题(每小题8分，共16分)

  • 23.  如图，四边形ABCD是平行四边形，∠BAD，∠ADC的平分线分别交DC，AB于点M，N，AM与DN相交于点H．

    (1)、求证AM⊥DN；
    (2)、连接MN，则四边形ANMD的形状为(填特殊四边形)；
    (3)、若BC=5，DN=6，直接写出AM的长为 ．

    查看试题解析

  • 24.  一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8 min内既进水又出水，每分的进水量和出水量是两个常数. 容器内的水量y(单位：L)与时间x(单位：min)之间的关系如图所示. 

    (1)、当0≤x≤4时，求y关于x的函数解析式；
    (2)、当4≤x≤12时，求y关于x的函数解析式；
    (3)、该容器每分进水L；每分出水L. 

    查看试题解析

六、解答题(每小题10分，共20分)

  • 25.  如图，在△ABC中，点P是边AC上一个动点，过点P作直线l∥AB. 设直线l交∠DAC的平分线于点M，交∠BAC的平分线于点N. 

    (1)、求证PM=PN；
    (2)、若AN=2，AM=1，求MN的值；
    (3)、当点P为AC的中点时，连接CM，CN，判断四边形ANCM的形状，并说明理由. 

    查看试题解析

  • 26.  如图1，正方形ABCD的边长为4，连接AC. 动点P从点A出发，以每秒1个单位的速度沿线段AB向终点B运动，过点P作PE⊥AB交AC于点E．以PE为一边向右作正方形PEFG．设点P的运动时间为x秒．正方形PEFG与正方形ABCD重叠部分图形的面积为y. 

    (1)、当x=1时，y=；
    (2)、当点F落在BC上时，x=；
    (3)、当x=3时，在图2中画出图形，并求出y的值；
    (4)、连接CF，当△CEF是等腰三角形时，直接写出x的值．

    查看试题解析