吉林省吉林市丰满区2022-2023学年七年级下学期期末考试数学试题
试卷更新日期：2023-07-24 类型：期末考试
一、单项选择题(每小题2分，共12分)
-
1. 实数81的算术平方根是（ ）A、9 B、±9 C、-9 D、32. 下列选项中，是二元一次方程的是（ ）A、a+3=5 B、x+y2=1 C、m+n=3 D、xy=63. 在平面直角坐标系中，点(-2，a2+3)一定在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知m<n，下列不等式不一定成立的是（ ）A、m+1<n+1 B、-3m>-3n C、m-5<n-5 D、ma>na5. 如图，这是小明同学在体育课上跳远成绩的示意图，即AM的长为小明同学的跳远成绩，其依据是（ ）
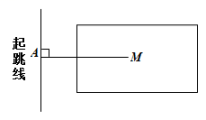A、过一点有且只有一条直线与已知直线垂直 B、两点确定一条直线 C、垂线段最短 D、两点之间线段最短6. 将△ABC沿AB方向平移到△EFD的位置，若∠1=31°，∠2=57°，则∠D的度数为（ ）
A、91° B、90° C、92° D、105°二、填空题(每小题3分，共24分)
-
7. 已知方程x+2y=10，用含y的代数式表示x，则x=.8. 命题“如果x2=9，那么x=3”是命题(填“真”或“假”).9. 为了解一批灯泡的使用寿命，选择的调查方式为(填“全面调查”或“抽样调查”).10. 介于整数n和n+1之间，则n的值是.11. 若点M(2a，a+3)在x轴上，则点M的坐标为.12. 在平面直角坐标系中，将点A(x，y)向左平移5个单位长度，再向上平移3个单位长度后与点B(-3，2)重合，则点A的坐标是.13. 如图，AB∥CD，∠C=55°，则∠1的度数是.
14. 如图，在平面直角坐标系中，直径为1个单位长度的圆从原点O出发，沿横轴向右滚动一周，圆上的一点由原点O到达点O'，圆心由点M到达点M'，则点M'对应的坐标是.
三、解答题(每小题5分，共20分)
-
15. 计算：16. 用加减法解方程组：17. 解不等式 ， 并在数轴上表示解集.
18. 解不等式组：四、解答题(每小题7分，共28分)
-
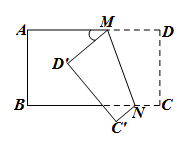
19. 已知3a的平方根是±3，5是3a-b的立方根，求2a-b的值.20. (我国古代问题)有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛(hú)，1个大桶加上5个小桶可以盛酒2斛，1个大桶1个小桶分别可以盛酒多少斛？21. 我们规定的运算法则为 ， 例如. 若 ， 求的取值范围.22. 如图，把一个长方形ABCD纸片沿MN折叠后，点D，C分别落在D'，C'的位置，若∠MNB=70°，求∠AMD'的度数．
五、解答题(每小题8分，共16分)
-
23. 某学校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文化类、天文类、社科类、历史类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），请根据图中信息，解答下列问题：
(1)、此次共调查了名学生；(2)、将条形统计图补充完整；(3)、图2中“天文类”所在扇形的圆心角为度；(4)、若该校共有学生900人，估计该校喜欢“文化类”书籍的学生人数.24. 如图，△ABC在平面直角坐标系中.
(1)、直接写出△ABC各顶点的坐标分别为A ， B ， C；(2)、若把△ABC向右平移1个单位长度，再向上平移3个单位长度得到△A'B'C'，在坐标系中画出平移后的图形；(3)、直接写出△ABC的面积为.六、解答题(每小题10分，共20分)
-
25. 用3辆A型车和2辆B型车装满货物一次可运货17吨；用2辆A型车和3辆B型车装满货物一次可运货18吨. 某物流公司现有38吨货物，计划同时租用A型车m辆，B型车n辆，一次运完，且恰好每辆车都装满货物.根据以上信息，解答下列问题：(1)、1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)、请你帮助该物流公司设计租车方案；(3)、若A型车每辆需租金100元/次，B型车每辆需租金120元/次，直接写出最省钱的租车方案为 ， 最低租车费为元.26. 如图，点A的坐标为(m，0)，点B在y轴上，将△ABO沿x轴正方向平移，平移后的图形为△CDE，点D的坐标为(n，2)，且 ．
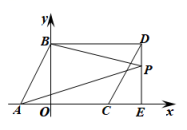(1)、点A的坐标为；点D的坐标为；(2)、点P从点B出发，以每秒1个单位的速度沿折线B→D→E向终点E运动，设点P的运动时间为t秒，回答下列问题：①当t = ▲ 时，点P的横坐标与纵坐标相等；
②当3﹤t﹤5时，请写出∠PBD，∠PAE，∠APB之间的数量关系，并说明理由；
③当直线AP将四边形ABDE的面积分成2∶5两部分时，直接写出t的值．