吉林省白山市江源区2022-2023学年七年级下学期数学期末试卷
试卷更新日期:2023-07-24 类型:期末考试
一、选择题(每小题2分,共12分)
-
1. 下列四个实数中是无理数的是( )A、π B、1.414 C、0 D、2. 平面直角坐标系中,点(-8,2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 不等式组的整数解的个数是( )
A、1个 B、2个 C、3个 D、4个4. 如图,下列判断中正确的是( ) A、如果EF∥GH,那么∠4+∠3=180° B、如果AB∥CD,那么∠1+∠4=180° C、如果AB∥CD,那么∠1=∠2 D、如果AB∥CD,那么∠2=∠35. 已知x < y,则下列不等式一定成立的是( )A、- x<- y B、3x < 4y C、6-x<6-y D、x-2<y-26. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式
A、如果EF∥GH,那么∠4+∠3=180° B、如果AB∥CD,那么∠1+∠4=180° C、如果AB∥CD,那么∠1=∠2 D、如果AB∥CD,那么∠2=∠35. 已知x < y,则下列不等式一定成立的是( )A、- x<- y B、3x < 4y C、6-x<6-y D、x-2<y-26. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式二、填空题(每小题3分,共24分)
-
7. 已知方程4x+5y-4=0,用含x的代数式表示y的形式,则。8. 如图,已知AB∥ED,∠ECF=65°,则∠BAF的度数为。
 9. 已知(a﹣1)2+|b+1|+ =0,则a+b+c= .10. 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到CD,若点
9. 已知(a﹣1)2+|b+1|+ =0,则a+b+c= .10. 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到CD,若点C的坐标为(6,3),则点D的坐标为。
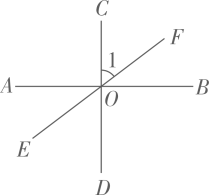
 11. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根为12. 如图,已知AB⊥CD,垂足为点O,直线EF经过O点,若∠1=55°,则∠AOE的
11. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根为12. 如图,已知AB⊥CD,垂足为点O,直线EF经过O点,若∠1=55°,则∠AOE的度数为度。
 13. 已知二元一次方程2x-3y =10,若x与y互为相反数,则x的值是。14. 若关于x的不等式组的整数解共有4个,则a的取值范围是。
13. 已知二元一次方程2x-3y =10,若x与y互为相反数,则x的值是。14. 若关于x的不等式组的整数解共有4个,则a的取值范围是。三、解答题(每小题5分,共20分)
-
15. 计算: -(1-)+|-|16. 解不等式+1,并把解集在数轴上表示出来。17. 如图,已知∠1+∠2=180°,∠B=∠3,求证:DE∥BC。
 18. 解方程组:
18. 解方程组:四、解答题(每小题7分,共28分)
-
19. 在平面直角坐标系中,△ABC的位置如图所示,把△ABC先向左平移2个单位,再向下平移4个单位可以得到△A′B′C′.

⑴画出三角形△A′B′C′,并写出A′,B′,C′三点的坐标;
⑵把△ABC还可以经过怎样的平移得到△A′B′C′,写出平移的方法.
20. 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,求每个小长方形的长和宽分别是多少? 21. 已知正数m的两个不同的平方根分别为a+5和-2a-2.(1)、求a的值(2)、求m的立方根22. 某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
21. 已知正数m的两个不同的平方根分别为a+5和-2a-2.(1)、求a的值(2)、求m的立方根22. 某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)、 在扇形统计图中,“玩游戏”对应的百分比为 , 圆心角度数是度;(2)、补全条形统计图;(3)、该校共有学生2100人,估计每周使用手机时间在2小时以上(不含2小时)的人数五、解答题(每小题8分,共16分)
-
23. 如图,已知在直角坐标系中,A(a,0),B(b,-2),C(1,c)三点,其中a,b满足关系式|a+2|++(c-4)2=0.
 (1)、请求出a,b,c的值,并在图中标出A,B,C三个点;(2)、在(1)的图中,连接AB,BC,AC,得到△ABC,请求出△ABC的面积.24. 在直角坐标系中,已知点P(2m+4,m-1)(1)、若点P的纵坐标比横坐标大3 ,则点P的坐标为;(2)、若点P到两坐标轴的距离相等 ,则点P的坐标为;(3)、若点P在过点A(2,-5) ,且与x轴平行的直线上,求点P的坐标。
(1)、请求出a,b,c的值,并在图中标出A,B,C三个点;(2)、在(1)的图中,连接AB,BC,AC,得到△ABC,请求出△ABC的面积.24. 在直角坐标系中,已知点P(2m+4,m-1)(1)、若点P的纵坐标比横坐标大3 ,则点P的坐标为;(2)、若点P到两坐标轴的距离相等 ,则点P的坐标为;(3)、若点P在过点A(2,-5) ,且与x轴平行的直线上,求点P的坐标。六、解答题(每小题10分,共20分)
-
25. 为积极响应政府提出的“绿色发展•低碳出行”号召,某社区决定购置一批共享单车。经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元。(1)、求男式单车和女式单车的单价;(2)、该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有哪几种购置方案?26. 如图,在平面直角坐标系中,点A、B是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足(a+b-32)2+|b-a+16|=0,将点B向左平移18个单位长度得到点C.
 (1)、求点A、B、C的坐标;(2)、点M、N分别为线段BC、OA上的两个动点,点M从点B以1个单位长度/秒的速度向左运动,同时点N从点A以2个单位长度/秒的速度向右运动,设运动时间为t秒(0≤ t ≤12).
(1)、求点A、B、C的坐标;(2)、点M、N分别为线段BC、OA上的两个动点,点M从点B以1个单位长度/秒的速度向左运动,同时点N从点A以2个单位长度/秒的速度向右运动,设运动时间为t秒(0≤ t ≤12).①当BM=ON时,求t的值;
②是否存在一段时间,使得S四边形NACM <S四边形BOAC?若存在,求出t的取值范围;若不存在请说明理由.