吉林省长春市榆树市2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-07-24 类型:期末考试
一、选择题(本大题共8小题,共24.0分。)
-
1. 下列方程为一元一次方程的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元一次方程的解是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、
3. 一元一次方程的解是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列正多边形中和正三角形组合,不能铺满地面的是( )A、正方形 B、正八边形 C、正十二边形 D、正六边形6. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、
5. 下列正多边形中和正三角形组合,不能铺满地面的是( )A、正方形 B、正八边形 C、正十二边形 D、正六边形6. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、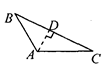 B、
B、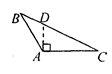 C、
C、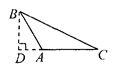 D、
D、 7. 下列生活实例中,利用了“三角形稳定性”的是( )A、
7. 下列生活实例中,利用了“三角形稳定性”的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,已知点是的边上一个动点, , 的面积为 , 则的长度的最小值是( )
8. 如图,已知点是的边上一个动点, , 的面积为 , 则的长度的最小值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
9. 把方程改写成用含x的式子表示y的形式,则 .10. 将“a的2倍与4的差是非负数”用不等式表示为.11. △ 的两边长分别是2和5,且第三边为奇数,则第三边长为.12. 将一副直角三角尺如图放置,则的大小为度.
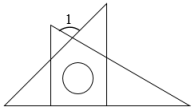 13. 如图, , 若 , 则度.
13. 如图, , 若 , 则度.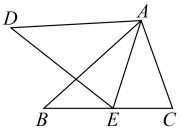 14. 如图,把绕点顺时针旋转得到 , 此时于 , 已知 , 则的度数是
14. 如图,把绕点顺时针旋转得到 , 此时于 , 已知 , 则的度数是
三、解答题(本大题共10小题,共78.0分。)
-
15.(1)、解方程: .(2)、解不等式:.16. 解方程组:17. 解不等式组:并写出它的所有整数解.18. 已知正多边形每个内角与它的外角的差为 , 求这个多边形内角的度数和边数.19. 如图,在中,于 , 平分交于点 , , , 求的度数.

请完善解答过程,并在括号内填写相应的理论依据.
解: ,
▲ 等式的性质 .
平分已知 ,
▲ ▲
已知 ,
▲ .
,
▲ ▲ .
20. 图、图均是的方格纸,的顶点均在格点上,只用无刻度的直尺,在给定的网格中按要求作图,保留适当的作图痕迹. (1)、在图中,画出 , 使和关于点成中心对称.(2)、在图中,将绕点顺时针旋转 , 画出旋转后的 .21. 如图,沿着的方向平移至 , , .
(1)、在图中,画出 , 使和关于点成中心对称.(2)、在图中,将绕点顺时针旋转 , 画出旋转后的 .21. 如图,沿着的方向平移至 , , . (1)、求的度数;(2)、若的周长为 , 平移距离为则四边形的周长为 .22. 问题解决:糖葫芦一般是用竹签串上山楂.再蘸以冰糖制作而成,现将一些山楂分别串在若干个竹签上,如果每根竹签串4个山楂,还剩余3个山楂;如果每根竹签串7个山楂,还剩余6根竹签,求竹签有多少根?山楂有多少个?反思归纳:现有m根竹签,n个山楂,若每根竹签串a个山楂,还剩b个山楂,则m、n、a、b满足的等量关系为(用含m、n、a、b的代数式表示).
(1)、求的度数;(2)、若的周长为 , 平移距离为则四边形的周长为 .22. 问题解决:糖葫芦一般是用竹签串上山楂.再蘸以冰糖制作而成,现将一些山楂分别串在若干个竹签上,如果每根竹签串4个山楂,还剩余3个山楂;如果每根竹签串7个山楂,还剩余6根竹签,求竹签有多少根?山楂有多少个?反思归纳:现有m根竹签,n个山楂,若每根竹签串a个山楂,还剩b个山楂,则m、n、a、b满足的等量关系为(用含m、n、a、b的代数式表示). 23. 如图
23. 如图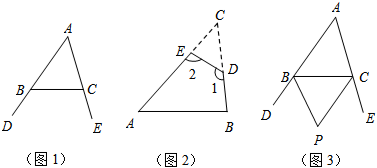
旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相部的两个外角的和之间存在怎样的数量关系呢?
(1)、尝试探究:如图 , 与分别为的两个外角,试探究与之间存在怎样的数量关系?为什么?(2)、初步应用:①如图 , 在纸片中剪去 , 得到四边形 , , 则 ▲ ;②小明联想到了曾经解决的一个问题:如图 , 在中,、分别平分外角、 , 与有何数量关系直接写出结论 .
24. 已知数轴上的原点为 , 、、三点对应的数分别为 , 和 , 动点从点出发,以每秒个单位的速度沿数轴正方向运动,同时,动点从点出发,以每秒个单位的速度沿数轴负方向运动,设点的运动时间为秒. (1)、线段的长为 , 线段的长为 .(2)、当点运动到与点、距离相等时,求点表示的数.(3)、当、两点相遇时,求的值.(4)、当时,直接写出的值.
(1)、线段的长为 , 线段的长为 .(2)、当点运动到与点、距离相等时,求点表示的数.(3)、当、两点相遇时,求的值.(4)、当时,直接写出的值.