吉林省吉林市船营区2022-2023学年七年级下学期期末考试数学试题

试卷更新日期：2023-07-24 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 36的平方根是（）

A、-6 B、6 C、± $\sqrt{6}$ D、±6

查看试题解析
2. 下列调查中，适宜采用全面调查方式的是（）

A、调查市场上奶制品的质量情况 B、了解全市中学生课外阅读的情况 C、调查乘坐飞机的旅客是否携带了违禁物品 D、了解船营区中学生的视力情况

查看试题解析
3. 在下列各数中 $\frac{22}{7}$ ，0.101001， $\sqrt{36}$ ， $\sqrt{3}$ ，无理数是（）

A、 $\frac{22}{7}$ B、0.101001 C、 $\sqrt{36}$ D、 $\sqrt{3}$

查看试题解析
4. 如图，AD与BC相交于点O，AB∥CD，如果 ∠B=20°，∠D=40° ，那么∠AOC的度数为（）

A、80° B、60° C、40° D、20°

查看试题解析
5. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为（4，3），（-2，1），则表示棋子“炮”的点的坐标为（）

A、（-3，3） B、（0，3） C、（1，3） D、（3，2）

查看试题解析
6. 如图，两个正方形的面积分别为25和16，两阴影部分的面积分别为 $a$ 和 $b$ $(a > b)$ ，则 $a - b$ 的算术平方根为（）

A、3 B、 $2 \sqrt{2}$ C、 $\sqrt{7}$ D、 $\sqrt{6}$

查看试题解析

二、填空题（每空3分，共24分）

7. 计算 $\sqrt[3]{- \frac{27}{8}} + \sqrt{\frac{1}{4}}$ =.

查看试题解析
8. 若 ${\begin{array}{l} x = 1 \\ y = － 2 \end{array}$ 是关于x和y的二元一次方程ax+y=1的解，则a的值等于．

查看试题解析
9. 如图，直线a，b被直线c所截，并且a∥b，若∠1=108°，则∠2的度数是．

查看试题解析
10. 如图，某单位要在河岸l上建一个水泵房引水到C处．他们的做法是：过点C作
CD⊥于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是．

查看试题解析
11. 若点 $（ m - 4 ， 1 - 2 m)$ 在第三象限内，则 $m$ 的取值范围是.

查看试题解析
12. 线段CD是由线段AB平移得到的，其中点A（3，-2）平移到点C（-1，4），点B（5，-8）平移到点D，则点D的坐标是．

查看试题解析
13. 如图，某人从点A沿北偏东60°的方向行走到点B，再从点B沿南偏西20°方向行走到点C，则∠ABC的度数为．

查看试题解析
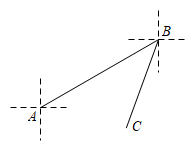14. 如图，由5个边长为1的小正方形组成的图片，可以把它剪拼成一个正方形，则拼成的正方形的边长是．

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算： $\sqrt{0.25} + | \sqrt{2} - 2 | - \sqrt[3]{27}$ .

查看试题解析
16. 解方程组： ${\begin{array}{l} 9 x + 4 y = 14 \\ 3 x - 2 y = 8 \end{array}$ ．

查看试题解析
17. 求不等式 $x + 1$ ≥ $2 x - 2$ 的非负整数解.

查看试题解析
18. 在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线
AB，CD，并说出自己做法的依据．小聪、小明、小智三位同学的做法如下：
小聪说：“我的做法的依据是内错角相等，两直线平行”
小聪说的是否正确？      ▲            ；（回答正确或错误）
小明做法的依据是      ▲            ；
小智做法的依据是      ▲            .

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，这是某市的部分简图（图中小正方形的边长代表1km长）.

(1)、请以火车站为坐标原点，建立平面直角坐标系；

(2)、分别写出其它各地的坐标：市场，宾馆，体育场，医院，超市.

查看试题解析
20. 为弘扬中华优秀传统文化，某校开展了“经典雅韵”诵读比赛活动，现随机抽取部
分同学的成绩进行统计，并绘制如下两个不完整的统计图，请结合图中提供的信息，解答下列各题：

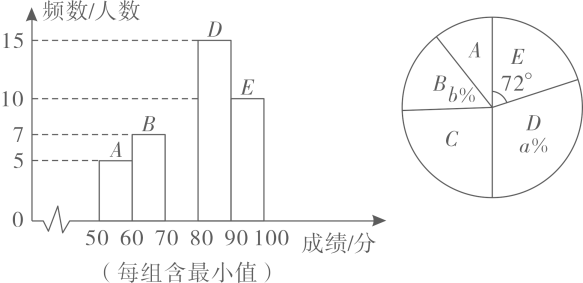(1)、填空：a＝， b=；

(2)、补全频数分布直方图；

(3)、如果全校有2000名学生参加这次活动，90分以上(含90分)为优秀，那么估计获得优秀奖的学生有多少人?

查看试题解析
21. 解不等式组： ${\begin{array}{l} － 2 x \leq 6 ① \\ x ＞－ 2 ② \\ 3 (x － 1) ＜ x + 1 ③ \end{array}$
请结合题意，完成本题的解答.

(1)、解不等式①，得，依据是：；

(2)、解不等式③，得；

(3)、把不等式①，②和③的解集在数轴上表示出来：

(4)、从图中可以找出三个不等式解集的公共部分，得不等式组的解集为.

查看试题解析
22. 我国古代数学著作《九章算术》中有下列问题：原文为“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何，” 意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛(斛：古代的一种容量单位)，1个大桶加上5个小桶可以盛酒2斛.求1个大桶、1个小桶分别可以盛酒多少斛？

查看试题解析

五、解答题（每小题8分,共16分）

23. 阅读下面材料，解答问题.
分母中含有未知数的不等式叫做分式不等式，如 $\frac{x - 2}{x + 1} > 0 ， \frac{2 x + 3}{x - 1} < 0$ 等.如何求出它们的解集呢？通过学习我们知道：数与式具有通性.根据我们学过的有理数的除法法则可知：两数相除，同号得正，异号得负.其字母表达式为：

(1)、①若 $a > 0 ， b > 0$ ，则 $\frac{a}{b} > 0$ 或若 $a < 0 ， b < 0$ ，则 $\frac{a}{b} > 0$ ；
②若 $a > 0 ， b < 0$ ，则 $\frac{a}{b} < 0$ 或若 $a < 0 ， b > 0$ ，则 $\frac{a}{b} < 0$ ；

反之，①若 $\frac{a}{b} > 0$ ，则 ${\begin{array}{l} a > 0 \\ b > 0 \end{array}$ 或 ${\begin{array}{l} a < 0 \\ b < 0 \end{array}$ .②若 $\frac{a}{b} < 0$ ，则或.

(2)、根据上述规律，求分式不等式 $\frac{x - 2}{x + 1} > 0$ 的解集.

查看试题解析
24. 如图，已知：DC∥FP，∠1=∠2，∠DEF=30°，∠AGF=80°，FH平分∠EFG．

(1)、求证：DC∥AB；

(2)、求∠PFH的度数．

查看试题解析

六、解答题（每小题10分，共20分）

25. 如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点
A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，
D，连接AC，BD，CD.

(1)、直接写出点C，D的坐标为C（），D（）；

(2)、四边形ABDC的面积为；

(3)、动点P从点A出发，沿折线AO－OC－CD以每秒1个单位长的速度向终点D运动，运动时间为x(s).当三角形PAC的面积与三角形POB的面积相等时，求点P运动时间x的值.

查看试题解析
26. 2023年5月31日，某校举办了首届初一年级学生“数学古文化阅读展示”活动，
为表彰在本次活动中表现优秀的学生，学校决定在6月1日购买笔袋或彩色铅笔作为奖品．已知1个笔袋，2筒彩色铅笔共需44元；2个笔袋，3筒彩色铅笔共需73元．解答下列各题：

(1)、每个笔袋、每筒彩色铅笔各多少元？

(2)、时逢“六一儿童节”，商店举行优惠促销活动，具体办法如下：笔袋“九折”优惠；彩色铅笔不超过10筒不优惠，超出10筒的部分“八折”优惠．若买x个笔袋需要y₁元，买x筒彩色铅笔需要y₂元．当x>10时，请用含x的式子表示y₁ ， y₂；

(3)、若在（2）的条件下购买同一种奖品95件，请你分析买哪种奖品省钱．

查看试题解析