安徽省阜阳市颍州区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数的解析式中是一次函数的是（）

A、y= $\frac{1}{- x}$ B、y= $\frac{1}{5}$ x+1 C、y=x²+1 D、y= $\sqrt{x}$

查看试题解析
2. 某校规定学生的学期数学成绩满分为100分，其中研究性学习成绩占40%，期末卷面成绩占60%，小明的两项成绩（百分制）依次是80分，90分，则小明这学期的数学成绩是（）

A、80分 B、82分 C、84分 D、86分

查看试题解析
3. 若一组数据3、4、5、x、6、7的平均数是5，则x的值是（）

A、5 B、6 C、7 D、8

查看试题解析
4. 如图，小明将一张长为20cm，宽为15cm的长方形纸(AE>DE)剪去了一角，量得AB=3cm，CD=4cm，则剪去的直角三角形的斜边长为（）

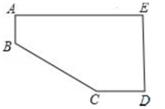A、5cm B、12cm C、16cm D、20cm

查看试题解析
5. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼，她连续、匀速走了60min后回家，图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s（km）与行走时间t（min）之间的函数关系，则下列图形中可以大致描述蕊蕊妈妈行走的路线是（）

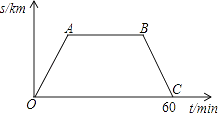A、 B、 C、 D、

查看试题解析
6. 为了了解某小区居民的用水情况，随机抽查了10户家庭的用水量，结果如下表：则关于这10户家庭的月用水量，下列说法错误的是（）
月用水量（吨）
4
5
6
9
户数
3
4
2
1

A、中位数为5吨 B、极差是3吨 C、众数是5吨 D、平均数是5.3吨

查看试题解析
7. 如图， $▱ A B C D$ 的对角线 $A C ， B D$ 交于点 $O$ ，已知 $A D = 8$ ， $B D = 12$ ， $A C = 6$ ，则 $△ O B C$ 的周长为（　　）

A、 $13$ B、 $15$ C、 $17$ D、 $26$

查看试题解析
8. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）

A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE

查看试题解析
9. 已知直线 $y = k x + b$ 经过一、二、四象限，则直线 $y = b x - k$ 的图象只能是（）

A、 B、 C、 D、

查看试题解析
10.
在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，图中的折线段表示甲、乙两车之间的距离y（千米）与行驶时间x(小时)的函数关系的图象.下列说法错误的是（）

A、乙先出发的时间为0.5小时 B、甲的速度是80千米/小时 C、甲出发0.5小时后两车相遇 D、甲到B地比乙到A地早 $\frac{1}{12}$ 小时

查看试题解析

二、填空题

11. 计算： $\sqrt{3} \times \sqrt{6} - \sqrt{8}$ = ．

查看试题解析
12. 为了建设“书香校园”，某校七年级的同学积极捐书，下表统计了七(1)班40名学生的捐书情况：

捐书(本)

3

4

5

7

10

人数

5

7

10

11

7

该班学生平均每人捐书本．

查看试题解析
13. 若关于 $x$ 的一次函数 $y = k x + b$ 的图象经过点 $A (- 1 ， 0)$ ，则方程 $k (x + 2) + b = 0$ 的解为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = 13$ ， $B C = 12$ ，点D，E分别是 $A B$ ， $B C$ 的中点，连接 $D E$ ， $C D$ ，若 $D E = 2.5$ ，则：

(1)、 $∠ D E B$ 的度数为；

(2)、 $△ A C D$ 的周长是．

查看试题解析

三、解答题

15. 计算： $(\sqrt{5} - \sqrt{2}) (\sqrt{5} + \sqrt{2}) + (\sqrt{3} - 1)^{2}$ ．

查看试题解析
16. 已知点 $(- 4 ， 2)$ 在正比例函数 $y = k x$ 的图象上.

(1)、求该正比例函数的解析式；

(2)、若点 $(- 1 ， m)$ 在函数 $y = k x$ 的图象上，求出 $m$ 的值.

查看试题解析
17. 如图，菱形ABCD的对角线AC、BD相交于点O，BE∥AC，CE∥DB．求证：四边形OBEC是矩形．

查看试题解析
18. 法国数学家费尔马早在 $17$ 世纪就研究过形如 $x^{2} + y^{2} = z^{2}$ 的方程，显然，这个方程有无数组解．我们把满足该方程的正整数的解 $(x ， y ， z)$ 叫做勾股数．如 $(3 ， 4 ， 5)$ 就是一组勾股数．

(1)、请你再写出两组勾股数：，；

(2)、在研究直角三角形的勾股数时，古希腊的哲学家柏拉图曾指出：如果 $n$ 表示大于1的整数， $x = 2 n$ ， $y = n^{2} - 1$ ， $z = n^{2} + 1$ ，那么，以 $x ， y ， z$ 为三边的三角形为直角三角形（即 $x ， y ， z$ 为勾股数），请你加以证明．

查看试题解析
19. 某社区为了解辖区群众对新冠疫情防控相关知识的知晓情况，通过发放问卷进行测评，从中随机抽取20份问卷，并统计成绩（成绩得分用x表示，单位：分），收集数据如下：
88 92 95 99 85 91 86 92 100 95 94 94 88 94 95 97 82 100 99 94
整理数据：

          $80 \leq x < 85$
          $85 \leq x < 90$
          $90 \leq x < 95$
          $95 \leq x \leq 100$
1
4
a
8
分析数据：

平均数
中位数
众数
93
b
94
根据以上信息，解答下列问题：

(1)、a= ， b=；

(2)、该社区有2000名群众参加了此次问卷测评活动，请估计成绩不低于90分的人数；

(3)、请从平均数和众数中选择一个量，结合本题解释它的意义．

查看试题解析
20. 如图，函数y＝﹣2x+3与y＝﹣ $\frac{1}{2}$ x+m的图象交于P（n，﹣2）．

(1)、求出m、n的值；

(2)、求出△ABP的面积．

查看试题解析

21. 我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．

	平均分 $（$ 分 $）$	中位数 $（$ 分 $）$	众数 $（$ 分 $）$	方差（ $分^{2}$ ）
初中部	$a$	$85$	$b$	$S_{初中}^{2}$
高中部	$85$	$c$	$100$	$160$

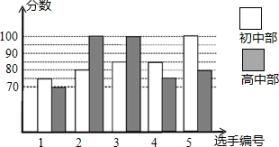(1)、根据图示计算出

a

、

b

、

c

的值；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算初中代表队决赛成绩的方差

s_{初 中}^{2}

，并判断哪一个代表队选手成绩较为稳定．

查看试题解析

22. 如图，在平行四边形ABCD中，点E ， F ， G ， H分别在边AB ， BC ， CD ， DA上，AE＝CG ， AH＝CF ，且EG平分∠HEF ．

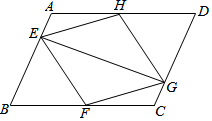(1)、求证：△AEH≌△CGF ．

(2)、若∠EFG＝90°．求证：四边形EFGH是正方形．

查看试题解析
23. 2021年3月20日，三星堆遗址考古新发现揭晓，出土文物500余件，三星堆考古发掘成果再次成为炙手可热的话题．某商家看准商机后，计划购进一批“考古盲盒”（三星堆文物模型盲盒）进行销售．已知该商家用1570元购进了10个甲种盲盒和15个乙种盲盒，甲种盲盒的进货单价比乙种盲盒的进货单价多2元．

(1)、甲种盲盒和乙种盲盒的进货单价分别是多少元；

(2)、由于“考古盲盒”畅销，商家决定再购进这两种盲盒共50个，其中甲种盲盒数量不多于乙种盲盒数量的2倍，且每种盲盒的进货单价保持不变．若甲种盲盒的销售单价为83元，乙种盲盒的销售单价为78元．
①假设此次购进甲种盲盒的个数为a（个），售完这两批盲盒所获总利润为w（元），请写出w与a之间的函数关系式；
②商家如何安排第二批进货方案，才能使售完这两批盲盒获得总利润最大？最大利润是多少元？

查看试题解析

$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x \leq 100$
1	4	a	8

月用水量（吨）	4	5	6	9
户数	3	4	2	1

捐书(本)	3	4	5	7	10
人数	5	7	10	11	7