安徽省合肥市蜀山区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-24 类型:期末考试
一、单选题
-
1. 如果在实数范围内有意义,那么x的取值范围是( )A、 B、 C、 D、2. 用配方法解方程 时,配方后得的方程是( )A、 B、 C、 D、3. 在中, , 则的面积为( )A、30 B、32.5 C、60 D、654. 如图,某校园内小池塘的岸边有 A、B两点,难以直接测量 A、B两点间的距离,数学实践活动小组的同学们在A、B外选择了一点C,取线段 , 的中点D,E,测得 , 则A、B两点的距离是( )
 A、 B、 C、 D、5. 方程根的符号是( )A、两根一正一负 B、两根都是负数 C、两根都是正数 D、无法确定6. 为了解某校学生青年大学习的情况,现安排一次竞赛活动,其中八年级某班有一些学生参加,最终成绩如下表, 关于这组数据不正确的是( )
A、 B、 C、 D、5. 方程根的符号是( )A、两根一正一负 B、两根都是负数 C、两根都是正数 D、无法确定6. 为了解某校学生青年大学习的情况,现安排一次竞赛活动,其中八年级某班有一些学生参加,最终成绩如下表, 关于这组数据不正确的是( )成绩/分
88
89
92
99
人数/人
2
3
4
1
A、平均数是91 B、众数是92 C、中位数是 90.5 D、方差是 987. 如图,在由边长为1个单位长度的小正方形组成的网格中,线段的两个端点都在正方形网格的格点上,则的长度可能是( ) A、 B、 C、 D、8. 如图,在平行四边形中, , 且 , , 经过中点O分别交、于点 M、N,连接、 , 则下列结论错误的是( )
A、 B、 C、 D、8. 如图,在平行四边形中, , 且 , , 经过中点O分别交、于点 M、N,连接、 , 则下列结论错误的是( ) A、四边形为平行四边形 B、当时,四边形为矩形 C、当时,四边形为菱形 D、四边形不可能为正方形9. 已知三个实数满足 , 则( )A、≥0 B、≤0 C、≥0 D、≤010. 如图,点E、F分别为矩形边、上的两点,连接、相交于点G,且 , 连接 , 则下列结论一定正确的是( )
A、四边形为平行四边形 B、当时,四边形为矩形 C、当时,四边形为菱形 D、四边形不可能为正方形9. 已知三个实数满足 , 则( )A、≥0 B、≤0 C、≥0 D、≤010. 如图,点E、F分别为矩形边、上的两点,连接、相交于点G,且 , 连接 , 则下列结论一定正确的是( ) A、 B、 C、 D、平分
A、 B、 C、 D、平分二、填空题
-
11. 实数 的整数部分是.12. 一个多边形的内角和与外角和的和是 ,那么这个多边形的边数n= .13. 关于的一元二次方程 , 有两个不相等的实数根,则的取值范围为.14. 如图,立在地上的旗杆 , 有一根绳子从杆顶 A 垂下,绳碰到地面后还余 4米,把绳的着地端沿地面移动到离旗杆底部 B点 10米处的一点C,恰好把绳子拉直, 则旗杆AB的高度为米.
 15. 某公司年的年产值为万元,年的年产值为万元,若这几年的年平均增长率相同,则该公司年的年产值是万元.16. 如图,在矩形中, , P为边上一动点,连接 , 把沿BP折叠使A落在处,当为等腰三角形时,的长为.
15. 某公司年的年产值为万元,年的年产值为万元,若这几年的年平均增长率相同,则该公司年的年产值是万元.16. 如图,在矩形中, , P为边上一动点,连接 , 把沿BP折叠使A落在处,当为等腰三角形时,的长为.
三、解答题
-
17. 计算:18. 解方程:19. 如图,在由边长为 1个单位长度的小正方形组成的网格中,点A,C均为格点(网格线的交点).
 (1)、若以为对角线,请在网格中画出一个菱形 (点B,D都在正方形网格的格点上);(2)、你所画出的菱形的面积是.20. 已知,如图,在中, , D是的中点, 连接 , F是的中点,过点C作交的延长线于点E,连接 . 求证:四边形是菱形.
(1)、若以为对角线,请在网格中画出一个菱形 (点B,D都在正方形网格的格点上);(2)、你所画出的菱形的面积是.20. 已知,如图,在中, , D是的中点, 连接 , F是的中点,过点C作交的延长线于点E,连接 . 求证:四边形是菱形. 21. 星空浩瀚无垠 ,探索永无止尽,某校在第八个中国航天日期间,举办了名为“星空遐想”的太空绘画展,并根据分数给画展上的作品评定等级,评定结果有分以下)四种,现从中随机抽取部分作品,对其结果进行整理,制成如图所示两幅不完整的统计图,
21. 星空浩瀚无垠 ,探索永无止尽,某校在第八个中国航天日期间,举办了名为“星空遐想”的太空绘画展,并根据分数给画展上的作品评定等级,评定结果有分以下)四种,现从中随机抽取部分作品,对其结果进行整理,制成如图所示两幅不完整的统计图,
请根据以上信息,完成下列问题:
(1)、本次共抽取了幅作品,扇形统计图中结果D所对应的扇形的圆心角为°;(2)、请补全频数分布直方图;(3)、已知该校共有2400名学生参加了本次画展,请估计评定结果为A的绘画作品大约有多少幅.22. 一种服装的进价为元/件,经销商经过市场调查发现该种服装如果销售单价为元/件,则年销售量为件,销售这种服装的员工每年工资以及其它费用总计元.(1)、用含的代数式表示每年销售这种服装的获利金额;注:每年获利金额=(销售单价-进价)×年销售量—其它费用.
(2)、若经销商希望该种服装一年的获利金额达元,且要使产品年销售量较大,你认为销售单价应定为多少元/件?23. 如图 1,在矩形中,点是边上一点,点 在 延长线上,且.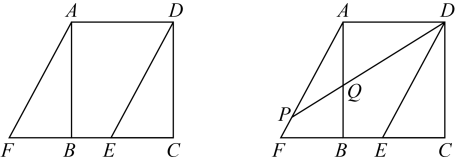 (1)、求证:四边形为平行四边形;(2)、如图2,在上取一点 , 使 , 连接 交于点 , 令=
(1)、求证:四边形为平行四边形;(2)、如图2,在上取一点 , 使 , 连接 交于点 , 令=①求的度数 (请用含的代数式表示);
②若 , 求证:四边形为正方形.