吉林省长春市榆树市八号镇2022-2023学年七年级下学期7月期末联考数学试题
试卷更新日期:2023-07-24 类型:期末考试
一、选择题(每题3分,共24分)
-
1. 若x2=4,则x的值是( )A、2 B、±2 C、16 D、±162. 在平面直角坐标系中,点P(-1,x2+1)(其中x为任意有理数)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列数中 , 0.101001, , , 无理数是( )A、 B、0.101001 C、 D、4. 不等式-2x+1<3的解集是( )A、
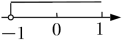 B、
B、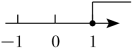 C、
C、 D、
D、 5. 我国明代数学读本《算法统宗》一书有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托。如果1托为5尺,那么索长和竿子长分别为多少尺?设索长为x尺,竿子长为y尺,可列方程组为( )A、 B、 C、 D、6. 下列图标既不是轴对称图形也不是中心对称图形的是( )A、
5. 我国明代数学读本《算法统宗》一书有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托。如果1托为5尺,那么索长和竿子长分别为多少尺?设索长为x尺,竿子长为y尺,可列方程组为( )A、 B、 C、 D、6. 下列图标既不是轴对称图形也不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,AC∥ED,∠C=26°,∠B=37°,则∠E的大小是( )
7. 如图,AC∥ED,∠C=26°,∠B=37°,则∠E的大小是( )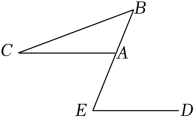 A、53° B、63° C、73° D、838. 如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )
A、53° B、63° C、73° D、838. 如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( ) A、α B、α-45° C、45°-α D、90°-α
A、α B、α-45° C、45°-α D、90°-α二、填空题(每题3分,共18分)
-
9. = .10. 不等式2x+4≤0的解集为 .11. 是关于x和y的二元一次方程ax+y=1的解,则a的值为 .12. 如图,在灌溉时,要把河中的水引到农田 处,并要求所挖的渠道最短,小明画线段 ,他的根据是.
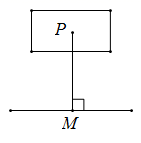 13. 如图所示的图案,至少要绕图案中心点旋转度后,才能与原来的图形重合.
13. 如图所示的图案,至少要绕图案中心点旋转度后,才能与原来的图形重合. 14. 如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为 .
14. 如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为 .

三、解答题(78分)
-
15. 计算:.16. 解方程组:17. 解不等式: , 并把解集在数轴上表示出来.18. 被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km.求隧道累计长度与桥梁累计长度.19. 利用平方根的意义求方程(x-1)2=4中x的值.20. 如图,在△ABC中,∠AED=80°,BD是∠ABC的平分线,DE∥BC,求∠EDB的度数.
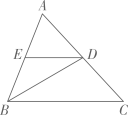 21. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作图,并保留必要的画图痕迹.
21. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作图,并保留必要的画图痕迹. (1)、在图①中画出关于直线l对称的图形.(2)、在图②中画出关于点O成中心对称的图形.(3)、在图③中,过点C画的垂线.22. 对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
(1)、在图①中画出关于直线l对称的图形.(2)、在图②中画出关于点O成中心对称的图形.(3)、在图③中,过点C画的垂线.22. 对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
 (1)、求∠EBC的度数;
(1)、求∠EBC的度数;解:∵CD⊥AB(已知),
∴∠CDB= ▲ °.
∵∠EBC=∠CDB+∠BCD( ).
∴∠EBC= ▲ °+35°= ▲ °(等量代换).
(2)、求∠A的度数.
∵∠EBC=∠A+∠ACB( ),∴∠A=∠EBC-∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A= ▲ -90°= ▲ °(等量代换).
23. 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.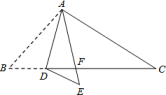 (1)、求∠AFC的度数;(2)、求∠EDF的度数.24. 我们在数学学习中,经常利用“转化”的思想方法解决问题,比如,我们通过“消元的方法将二元一次方程组转化为一元一次方程,从而求解.下面我们就利用“转化”的思想方法尝试解决新的问题.
(1)、求∠AFC的度数;(2)、求∠EDF的度数.24. 我们在数学学习中,经常利用“转化”的思想方法解决问题,比如,我们通过“消元的方法将二元一次方程组转化为一元一次方程,从而求解.下面我们就利用“转化”的思想方法尝试解决新的问题.先阅读下面的例题,再按要求完成下列问题.
例:解不等式(x-2)(x+1)>0.
解:由有理数的乘法法则“两数相乘,同号得正”,得①或②
解不等式组①,得x>2.
解不等式组②,得x<-1.
所以不等式(x-2)(x+1)>0的解集为x>2或x<-1.
根据例题方法解决下面问题:
(1)、解不等式(x+3)(2x-1)<0.解:由有理数的乘法法则“两数相乘,异号得负”,得①或② .
解不等式组①,得 .
解不等式组②,得 .
所以不等式(x+3)(2x-1)<0的解集为 .
(2)、应用:不等式:的解集为 .25. 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a-2|+(b-3)2+=0. (1)、求a、b、c的值;(2)、如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)、在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.
(1)、求a、b、c的值;(2)、如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)、在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.