河南省周口市沈丘县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-24 类型:期末考试
一、单选题(每小题3分,共30分)
-
1. 下列代数式中,属于分式的是( )A、 B、 C、 D、2. 为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为( )A、35×10﹣6 B、3.5×10﹣6 C、3.5×10﹣5 D、0.35×10﹣43. 在平面直角坐标系中,点P(﹣3,2)关于x轴的对称点的坐标为( )A、(2,﹣3) B、(﹣2,3) C、(﹣3,2) D、(﹣3,﹣2)4. 早上9点,甲车从地出发去地,20分钟后,乙车从地出发去地.两车离开各自出发地的路程(千米)与时间(小时)的函数关系如图所示,下列描述中不正确的是( )
 A、两地相距240千米 B、乙车平均速度是90千米/小时 C、乙车在12:00到达地 D、甲车与乙车在早上10点相遇5. 定义新运算: , 则对于函数 , 下列说法正确的是( ).A、y随x增大而减小 B、该函数图象经过点(-2,-4) C、当0<x<2时,0<y<4 D、该函数不经过第四象限6. 下列说法错误的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有三个角是直角的四边形是矩形 D、两组对边分别相等的四边形是平行四边形7. 下列说法不正确的是( )A、在选举中,人们通常最关心的数据是众数 B、数据3,5,4,1,﹣2的中位数是3 C、一组数据1,1,0,2,4的平均数为2 D、甲、乙两人数学成绩的平均分都是95,方差分别是2.5和10.5,要选择一人参加数学竞赛,选甲比较稳定8. 如图,四边形OABC是菱形,CD⊥x轴,垂足为D,函数的图象经过点C,若CD=4,则菱形OABC的面积为( )
A、两地相距240千米 B、乙车平均速度是90千米/小时 C、乙车在12:00到达地 D、甲车与乙车在早上10点相遇5. 定义新运算: , 则对于函数 , 下列说法正确的是( ).A、y随x增大而减小 B、该函数图象经过点(-2,-4) C、当0<x<2时,0<y<4 D、该函数不经过第四象限6. 下列说法错误的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有三个角是直角的四边形是矩形 D、两组对边分别相等的四边形是平行四边形7. 下列说法不正确的是( )A、在选举中,人们通常最关心的数据是众数 B、数据3,5,4,1,﹣2的中位数是3 C、一组数据1,1,0,2,4的平均数为2 D、甲、乙两人数学成绩的平均分都是95,方差分别是2.5和10.5,要选择一人参加数学竞赛,选甲比较稳定8. 如图,四边形OABC是菱形,CD⊥x轴,垂足为D,函数的图象经过点C,若CD=4,则菱形OABC的面积为( ) A、15 B、20 C、29 D、249. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状不可能是( )
A、15 B、20 C、29 D、249. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状不可能是( )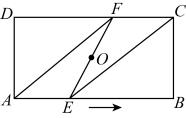 A、平行四边形 B、菱形 C、正方形 D、矩形10. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A、平行四边形 B、菱形 C、正方形 D、矩形10. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )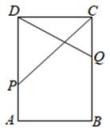 A、8 B、10 C、12 D、20
A、8 B、10 C、12 D、20二、填空题(每小题3分,共15分)
-
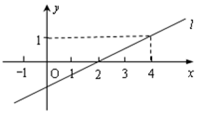
11. 要使分式有意义,则x的取值范围是;12. 如图,已知一次函数 的图象为直线,则关于 的方程 的解 .
 13. 已知点A(3,y1)、B(m,y2)是反比例函数的图象上的两点,且y1<y2 . 写出满足条件的m的一个值,m可以是 .14. 如图,正方形的对角线相交于点O,以O为顶点的正方形的两边 , 分别交正方形的边 , 于点M,N.记的面积为S1 , 的面积为S2 , 若正方形的边长 , S1=16,则S2的大小为 .
13. 已知点A(3,y1)、B(m,y2)是反比例函数的图象上的两点,且y1<y2 . 写出满足条件的m的一个值,m可以是 .14. 如图,正方形的对角线相交于点O,以O为顶点的正方形的两边 , 分别交正方形的边 , 于点M,N.记的面积为S1 , 的面积为S2 , 若正方形的边长 , S1=16,则S2的大小为 . 15. 在四边形ABCD中,AD∥BC,BC⊥CD,BC=10cm,M是BC上一点,且BM=4cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,当t的值为时,以A、M、E、F为顶点的四边形是平行四边形.
15. 在四边形ABCD中,AD∥BC,BC⊥CD,BC=10cm,M是BC上一点,且BM=4cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,当t的值为时,以A、M、E、F为顶点的四边形是平行四边形.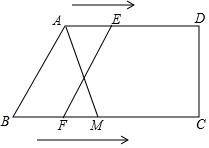
三、解答题(共75分)
-
16.(1)、计算:(2)、化简:.17. 某商店准备购进A,B两种护眼灯,已知每台护眼灯的进价A种比B种多40元,用2000元购进A种护眼灯和用1600元购进B种护眼灯的数量相同.(1)、A,B两种护眼灯每台进价各是多少元?(2)、该商店计划用不超过14550元的资金购进A,B两种护眼灯共80台,A,B两种护眼灯的每台售价分别为300元和200元.若这两种护眼灯全部售出,则该商店应如何进货才能获得最大利润?最大利润是多少?18. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表:
镜片焦距x(米)
1.00
0.50
0.25
0.20
0.10
近视眼镜的度数y(度)
100
200
400
500
1000
(1)、请写出适当的函数解析式描述近视眼镜的度数y与镜片焦距x的关系;(2)、验光师测得小明同学的近视度数是250度,给小明配的眼镜的焦距应该是多少米?19. 王老师为了选拔一名学生参加数学比赛,对两名备赛选手进行了10次测验,成绩如下(单位:分):甲:5,6,6,6,6,6,7,9,9,10,
乙:5,6,6,6,7,7,7,7,9,10;选手
平均数
中位数
众数
方差
甲
a
b
6 2.6
乙
7 7 c d
(1)、以上成绩统计分析表中a= , b= , c=;(2)、d2.6;(填“>”、“<”或“=”)(3)、根据以上信息,你认为王老师应该选哪位同学参加比赛,请说明理由.20. 如图,在菱形中,轴,点的坐标为 , 点的坐标为 , 边所在直线与轴交于点 , 与双曲线交于点 .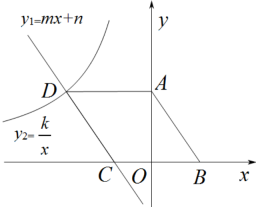 (1)、求直线的函数表达式及的值;(2)、把菱形沿轴的正方向平移多少个单位后,点落在双曲线上?(3)、直接写出使的自变量的取值范围.21. 下面是小东设计的“作矩形”的尺规作图过程.
(1)、求直线的函数表达式及的值;(2)、把菱形沿轴的正方向平移多少个单位后,点落在双曲线上?(3)、直接写出使的自变量的取值范围.21. 下面是小东设计的“作矩形”的尺规作图过程.已知:中,∠ABC=90°.
求作:矩形 .
作法:如图,
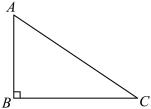
①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=OB
③连接AD,CD
所以四边形ABCD即为所求作的矩形
根据小东设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵OA= ▲ , OD=OB,
∴四边形ABCD是平行四边形( )(填推理的依据).
∵∠ABC=90°,
四边形ABCD是矩形( )(填推理的依据)
22. 如图,▱ABCD中,点E是CD的中点,连接AE并延长交BC延长线于点F.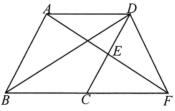 (1)、求证:CF=AD(2)、连接BD,DF,
(1)、求证:CF=AD(2)、连接BD,DF,①当∠ABC=90°时,△BDF的形状是;
②若∠ABC=50°,当∠CFD=°时,四边形ABCD是菱形.
23. 如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,-2),与直线CD交于点A(m,2).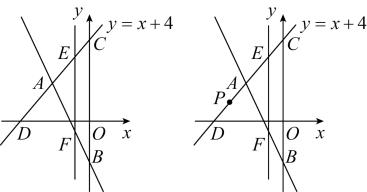 (1)、求直线AB的解析式;(2)、点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)、设P是射线CD上一动点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出符合条件的点Q的个数及其中一个点Q的坐标;否则说明理由.
(1)、求直线AB的解析式;(2)、点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)、设P是射线CD上一动点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出符合条件的点Q的个数及其中一个点Q的坐标;否则说明理由.