2023-2024学年北师大版数学七年级上册2.6有理数的加减混合运算（培优卷）

试卷更新日期：2023-07-24 类型：同步测试

进入出卷网下载

一、选择题

1. 下列变形，运用加法运算定律正确的是（）

A、3+(-2)=2+3 B、4+(-6)+3=(-6)+4+3 C、(5+(-2))+4=(5+(-4))+2 D、 $\frac{1}{6} + (- 1) + (+ \frac{5}{6}) = (\frac{1}{6} + \frac{5}{6}) + (+ 1)$

查看试题解析
2. 老师设计了接力游戏，用合作的方式完成有理数加减运算，规则是：每名同学只能利用前面一个同学的式子，进一步计算，再将结果传给下一个同学，最后解决问题，过程如图所示：

接力中，自己负责一步正确的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 已知a=|−30−42|，b=|−30|−|−42|，c=−30−|−42|，d=−|−30|−(−42)，则a、b、c、d的大小顺序为（　　）

A、d＜c＜b＜a B、c＜d＜b＜a C、b＜d＜c＜a D、c＜b＜d＜a

查看试题解析
4. 计算 $\frac{5}{6} - \frac{3}{8} + (- 2 \frac{7}{8})$ 的值为（）

A、 $- \frac{2}{3}$ B、 $- 2 \frac{5}{12}$ C、 $- 3 \frac{1}{24}$ D、 $- 14 \frac{11}{24}$

查看试题解析
5. 计算机中常用的十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数符号，这些符号与十进制的数的对应关系如下表：
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
0
0
3
4
5
6
7
8
9
10
11
12
13
14
15
例如，用十六进制表示E+D=1B，用十进制表示也就是13+14=1×16+11，则用十六进制表示A×B=（）

A、6E B、72 C、5F D、B0

查看试题解析
6. 在1、2、3、…99、100这100个数中，任意加上“+”或“-”，相加后的结果一定是（）

A、奇数 B、偶数 C、0 D、不确定

查看试题解析
7. 计算：1+( $-$ 2)+3+( $-$ 4)+…+2017+( $-$ 2018)的结果是（）

A、0 B、 $-$ 1 C、 $-$ 1009 D、1010

查看试题解析
8. 大家都知道，八点五十五可以说成九点差五分，有时这样表达更清楚．这启发人们设计一种新的加减计数法．
比如：9写成1 $\bar{1}$ ，1 $\bar{1}$ =10﹣1；
198写成20 $\bar{2}$ ， 20 $\bar{2}$ =200﹣2；
7683写成1 $\overset{____}{232}$ 3，1 $\overset{____}{232}$ 3=10000﹣2320+3
总之，数字上画一杠表示减去它，按这个方法请计算5 $\overset{__}{2}$ 3 $\overset{__}{1}$ ﹣3 $\overset{___}{24}$ 1=（）

A、1990 B、2068 C、2134 D、3024

查看试题解析
9. 如图，在日历中任意圈出一个3×3的正方形，则里面九个数不满足的关系式是（）

A、a₁+a₂+a₃+a₇+a₈+a₉=2（a₄+a₅+a₆） B、a₁+a₄+a₇+a₃+a₆+a₉=2（a₂+a₅+a₈） C、a₁+a₂+a₃+a₄+a₅+a₆+a₇+a₈+a₉=9a₅ D、（a₃+a₆+a₉）﹣（a₁+a₄+a₇）=（a₂+a₅+a₈）

查看试题解析
10. 已知有理数a，b，c，在数轴上的位置如图，下列结论错误的是（）

A、|a-b|=a-b B、a+b+c<0 C、 $- c - b + a < 0$ D、|c|-|a|+|-b|+|-a|=-c-b

查看试题解析

二、填空题

11. 如图所示是计算机程序计算，若开始输入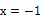，则最后输出的结果是；

查看试题解析
12. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第2次将点A₁向右平移6个单位长度到达点A₂ ，第3次将点A₂向左移动9个单位长度到达点A₃…则第6次移动到点A₆时，点A₆在数轴上对应的实数是；按照这种规律移动下去，至少移动次后该点到原点的距离不小于41．

查看试题解析
13. 计算： $| \frac{1}{2018} - \frac{1}{2017} | + | \frac{1}{2017} - \frac{1}{2016} | - | \frac{1}{2018} - \frac{1}{2016} | =$ .

查看试题解析
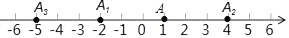14. 一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是个单位.

查看试题解析
15. 有理数a，b，c在数轴上的对应点如图所示，计算a－b＋c0(填“＞”“＜”或“＝”)．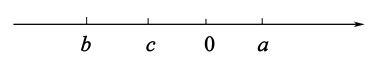

查看试题解析

三、解答题

16. 根据图示的对话解答下列问题．

求：

(1)、 $a$ ， $b$ 的值；

(2)、 $8 - a + b - c$ 的值．

查看试题解析
17. 设 A 是由 2×4 个整数组成的 2 行 4 列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．数表A 如下表所示，如果经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负整数，请写出每次“操作”后所得的数表．（写出一种方法即可）

1

2

3

－7

－2

－1

0

1

查看试题解析
18. 在数字：1、2、3、4、5、6、7、8、9、10、11、12、13的前面添上“+”或“﹣”能使其和为0吗？若能，请写出一个符合的算式，若不能，请说明理由；能使和为﹣3吗？若能，请写出一个符合的算式，若不能，请说明理由．

查看试题解析
19. 已知1- $\frac{1}{2}$ = $\frac{1}{2}$ ， $\frac{1}{2}$ - $\frac{1}{3}$ = $\frac{1}{6}$ ， $\frac{1}{3}$ - $\frac{1}{4}$ = $\frac{1}{12}$ ， $\frac{1}{4}$ - $\frac{1}{5}$ = $\frac{1}{20}$ ………根据这些等式求值。请你仔细观察，并找出其奥妙，再计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{49 \times 50}$

查看试题解析
20.

(1)、尝试：比较下列各式的大小关系：（用“＞，＜，＝，≥或≤”填空）
①|－2|＋|3| |－2＋3|；           ②|－6|＋|4||－6＋4|；

③|－3|＋|－4||－3－4|；        ④|0|＋|－7| |0－7|.

(2)、归纳：观察上面的数量关系，可以得到：|a|＋|b| |a＋b| （用“＞，＜，＝，≥或≤”填空）

(3)、应用：利用上面得到的结论解决下面问题：若|m|＋|n|＝10，|m＋n|＝4，则m＝ .

(4)、拓展：当|a|＋|b|＋|c|＞|a＋b＋c|成立时，a、b、c应满足的条件是（填写所有正确选项的序号） .
①1个正数，2个负数；    ②2个正数，1个负数；    ③3个正数；     ④3个负数；⑤1个0，2个正数；      ⑥1个0，2个负数；      ⑦1个0，1个正数，1个负数.

查看试题解析

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	0	0	3	4	5	6	7	8	9	10	11	12	13	14	15

1	2	3	－7
－2	－1	0	1