【备考2024年】中考数学杭州卷真题变式分层精准练第8题

试卷更新日期：2023-07-24 类型：二轮复习

进入出卷网下载

一、原题

1. 设二次函数 $y = a (x - m) (x - m - k) (a > 0 ， m ， k$ 是实数 $)$ ，则（）

A、当 $k = 2$ 时，函数 $y$ 的最小值为 $- a$ B、当 $k = 2$ 时，函数 $y$ 的最小值为 $- 2 a$ C、当 $k = 4$ 时，函数 $y$ 的最小值为 $- a$ D、当 $k = 4$ 时，函数 $y$ 的最小值为 $- 2 a$

查看试题解析

二、基础

2. 关于二次函数y＝﹣（x﹣2）²+3的最值，下列说法正确的是（）

A、有最大值2 B、有最小值2 C、有最大值3 D、有最小值3

查看试题解析
3. 关于二次函数 $y = - {(x - 1)}^{2} + 3$ 的最值，说法正确的是（）

A、最小值为-1 B、最小值为3 C、最大值为1 D、最大值为3

查看试题解析
4. 已知二次函数 $y = x^{2} - 4 x + 2$ ，当 $- 1 \leq x \leq 1$ 时，y的最小值为（）

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、7

查看试题解析
5. 二次函数 $y = - {(x + 1)}^{2} + 2$ ，当 $- 3 \leq x \leq 0$ 时， $y$ 的（）

A、最小值是1 B、最小值是0 C、最小值是-1 D、最小值是-2

查看试题解析
6. 在平面直角坐标系中，二次函数 $y = x^{2} + m x + m^{2} - m (m$ 为常数 $)$ 的图象经过点 $(0 ， 6)$ ，其对称轴在 $y$ 轴左侧，则该二次函数有（）

A、最大值 $5$ B、最大值 $\frac{15}{4}$ C、最小值 $5$ D、最小值 $\frac{15}{4}$

查看试题解析
7. 已知二次函数 $y = x^{2} - 4 x + 5$ ，关于该函数在 $a \leq x \leq 4$ 的取值范围内，下列说法项正确的是（）

A、若 $a < 0$ ，函数有最大值5 B、若 $a < 0$ ，函数有最小值5 C、若 $0 < a < 2$ ，函数有最小值1 D、若 $0 < a < 2$ ，函数无最大值

查看试题解析
8. 二次函数y = mx² - 4x + 1有最小值 - 3，则m等于（）

A、1 B、- 1 C、±1 D、 $\frac{1}{2}$

查看试题解析
9. 已知抛物线 $y = a x^{2} - 2 a x + 1 (α < 0)$ ，当 $- 1 \leq x \leq 2$ 时，y的最小值为 $- 2$ ，则当 $- 1 \leq x \leq 2$ 时，y的最大值为（）

A、2 B、1 C、0 D、 $- 1$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图像开口向下，顶点坐标为 $(3 ， - 7)$ ，那么该二次函数有（）

A、最小值-7 B、最大值-7 C、最小值3 D、最大值3

查看试题解析
11. 已知二次函数的图象（ $0 \leq x \leq 3.4$ ）如图．关于该函数在所给自变量的取值范围内，下列说法正确的是（）

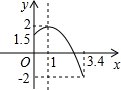A、有最大值2，无最小值 B、有最大值2，有最小值1.5 C、有最大值2，有最小值 $- 2$ D、有最大值1.5，有最小值 $- 2$

查看试题解析

三、提高

12. 已知二次函数 $y = x^{2} - 4 x + 2$ ，关于该函数在 $a \leq x \leq 3$ 的取值范围内有最大值-1，a可能为（）

A、-2 B、-1 C、0.5 D、1.5

查看试题解析
13. 当 $- 2 \leq x \leq 1$ 时，二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ 有最大值4，则实数m的值为（）

A、 $2 或 - \frac{7}{4}$ B、 $\sqrt{3} 或 - \sqrt{3}$ C、 $2 或 - \sqrt{3}$ D、 $2 或 \sqrt{3} 或 - \frac{7}{4}$

查看试题解析
14. 已知二次函数 $y = a x^{2} + 2 a x + 2 a^{2} + 5$ （其中x是自变量），当 $x \geq 2$ 时，y随x的增大而增大，且当 $- 2 ≤ x ≤ 1$ 时，y的最大值为10，则a的值为（）

A、1 B、 $- \sqrt{5}$ 或 $\sqrt{5}$ C、2.5 D、1或 $- 2.5$

查看试题解析
15. 已知二次函数 $y = - x^{2} + b x + c$ 的图象经过点 $(- 1 ， 0)$ ， $(2 ， 3)$ ，在 $a \leq x \leq 5$ 范围内有最大值为 $4$ ，最小值为 $- 12$ ，则 $a$ 的取值范围是（）

A、 $a \leq - 3$ B、 $- 3 \leq a \leq 1$ C、 $1 ≤ a ≤ 5$ D、 $a \geq 5$

查看试题解析
16. 已知二次函数 $y = a x^{2} - 2 a x + a + 2 （ a \neq 0 ）$ ，若 $- 1 \leq x \leq 2$ 时，函数的最大值与最小值的差为4，则a的值为（）

A、 $\pm \frac{4}{3}$ B、 $\pm 1$ C、 $- 1$ 或 $- \frac{4}{3}$ D、1或 $\frac{4}{3}$

查看试题解析
17. 在平面直角坐标系中，设二次函数 $y_{1} = x^{2} + 2 b x + a$ ， $y_{2} = a x^{2} + 2 b x + 1$ （a，b；是实数， $a \neq 0$ ）的最小值分别为m和n，若 $m + n = 0$ ，则 $m n$ 的值为（）

A、0 B、 $- 1$ C、 $- 2$ D、 $- 4$

查看试题解析
18. 已知二次函数 $y = - x^{2} + 2 c x + c$ 的图象经过点 $A (a ， c) ， B (b ， c)$ ，且满足 $0 < a + b < 2$ .当 $- 1 \leq x \leq 1$ 时，该函数的最大值m和最小值n之间满足的关系式是（）

A、 $n = - 3 m - 4$ B、 $m = - 3 n - 4$ C、 $n = m^{2} + m$ D、 $m = n^{2} + n$

查看试题解析
19. 已知非负数a，b，c，满足a-b=2且c+3a=9，设y=a²+b+c的最大值为m，最小值为n，则m﹣n的值是（）

A、1 B、2 C、3 D、4

查看试题解析
20. 已知二次函数 $y = (x - a)^{2} + 5 - a^{2}$ ，当 $2 a \leq x \leq 2 a + 2$ 时，有最大值 $y_{1}$ 及最小值 $y_{2}$ ，当 $y_{1} - y_{2} = a^{2} - 1$ 时，实数 $a$ 的值为（）

A、-3或-1或5 B、-3或5 C、-1或 $- \frac{5}{4}$ D、-3或 $- \frac{5}{4}$ 或5

查看试题解析
21. 规定 $m a x {a ， b} = {\begin{array}{l} a (a \geq b) \\ b (a \leq b) \end{array}$ ，若函数 $y = m a x {- 2 x + 1 ， x^{2} - 2 x - 3}$ ，则该函数的最小值为（）

A、 $- 3$ B、 $- 2$ C、2 D、5

查看试题解析
22. 已知二次函数y=（x-m+2）（x+m-4）+n，其中m，n为常数，则（）

A、m>1，n<0时，二次函数的最小值大于0 B、m=1，n>0时，二次函数的最小值大于0 C、m<1，n>0时，二次函数的最小值小于0 D、m=1，n<0时，二次函数的最小值小于0

查看试题解析
23. 定义：如果两个函数图象上至少存在一对点是关于原点对称的，我们则称这两个函数互为“守望函数”，这对点称为“守望点”.例如：点 $P (2 ， 4)$ 在函数 $y = x^{2}$ 上，点 $Q (- 2 ， - 4)$ 在函数 $y = - 2 x - 8$ 上，点P与点Q关于原点对称，此时函数 $y = x^{2}$ 和 $y = - 2 x - 8$ 互为“守望函数”，点P与点Q则为一对“守望点”.已知函数 $y = x^{2} + 2 x$ 和 $y = 4 x + n - 2022$ 互为“守望函数”，则n的最大值为（）

A、 $2020$ B、 $2022$ C、 $2023$ D、 $4084$

查看试题解析

四、培优

24. 已知抛物线 $y_{1} = x^{2}$ ，该抛物线经过平移得到新抛物线 $y_{2}$ ，新抛物线与x轴正半轴交于两点，且交点的横坐标在1到2之间，若点 $P (1 ， p)$ ， $Q (2 ， q)$ 在抛物线 $y_{2}$ 的图象上，则 $P Q$ 的范围是（）

A、 $0 \leq P Q < 1$ B、 $1 \leq P Q < 2$ C、 $1 \leq P Q < \sqrt{2}$ D、 $\sqrt{2} \leq P Q < 2$

查看试题解析
25. 已知抛物线 $y = {(x - b)}^{2} + c$ 经过 $A (1 - n ， y_{1})$ ， $B (n ， y_{2})$ ， $C (n + 3 ， y_{3})$ 三点， $y_{1} = y_{3}$ ．当 $1 - n \leq x \leq n$ 时，二次函数的最大值与最小值的差为16，则 $n$ 的值为（）

A、-5 B、3 C、 $\frac{19}{6}$ D、4

查看试题解析
26. 已知二次函数 $y = a x^{2} + 2 x + 1$ （a为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq x_{0}$ 的任意一个x的值，都有 $- 3 \leq y \leq 3$ ，则 $x_{0}$ 的最大值为（）

A、 $2 \sqrt{3} - 2$ B、 $2 \sqrt{3} + 2$ C、 $2 \sqrt{5} + 2$ D、 $2 \sqrt{5} - 2$

查看试题解析
27. 已知点A(x₁ ， y₁)，B(x₂ ， y₂)，C(x₃ ， y₃)，均在抛物线y=ax²-6ax+c，其中y₂=-9a+c.下列说法正确的是（）.

A、 $若 | x_{1} - x_{2} | \leq | x_{3} - x_{2} | ，则 y_{2} \geq y_{3} \geq y_{1}$ B、 $若 | x_{1} - x_{2} | \geq | x_{3} - x_{2} | ，则 y_{2} \geq y_{3} \geq y_{1}$ C、 $若 y_{1} > y_{3} \geq y_{2} ，则 | x_{1} - x_{2} | < | x_{2} - x_{3} |$ D、 $若 y_{1} > y_{3} \geq y_{2} ，则 | x_{1} - x_{2} | > | x_{2} - x_{3} |$

查看试题解析
28. 已知二次函数y＝x²+bx+c，当m≤x≤m+1时，此函数最大值与最小值的差（）

A、与m，b，c的值都有关 B、与m，b，c的值都无关 C、与m，b的值都有关，与c的值无关 D、与b，c的值都有关，与m的值无关

查看试题解析
29. 已知二次函数 $y = a x^{2} + b x - 1$ （a，b是常数， $a \neq 0$ ）的图象经过 $A (2 ， 1)$ ， $B (4 ， 3)$ ， $C (4 ， - 1)$ 三个点中的其中两个点.平移该函数的图象，使其顶点始终在直线 $y = x - 1$ 上，则平移后所得抛物线与y轴交点纵坐标的（）

A、最大值为-1 B、最小值为-1 C、最大值为 $- \frac{1}{2}$ D、最小值为 $- \frac{1}{2}$

查看试题解析
30. 如图，点A（1，16），B（2，12），C（3，8），D（4，4）均在函数l图象上，P为该函数在第一象限内图象上一点，PE⊥x轴于点E，当△OEP的面积取最大值时，OE的长为（）

A、1.5 B、2.5 C、3.5 D、4.5

查看试题解析