2023年中考数学真题分类汇编（全国版）：锐角三角函数（3）

试卷更新日期：2023-07-23 类型：二轮复习

进入出卷网下载

一、计算题

1. 先化简，再求值： $(m + 2 + \frac{5}{2 - m}) \cdot \frac{2 m - 4}{3 - m}$ ，其中 $m = \sqrt{16} - t a n 45 °$ ．

查看试题解析
2. 计算： $| - \sqrt{2} | + {(- 2023)}^{0} - 2 s i n 45 ° - {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
3. 计算： $| - \sqrt{3} | - (4 - π)^{0} - 2 s i n 60 ° + {(\frac{1}{5})}^{- 1}$ ．

查看试题解析
4. 计算： ${(\frac{1}{2})}^{- 1} - \sqrt{3} t a n 30 ° + {(π - 2023)}^{0} + | - 2 |$ ．

查看试题解析
5. 计算： $2 s i n 30 ° - 8 + {(2 - π)}^{0} + {(- 1)}^{2023}$

查看试题解析
6. 计算

(1)、计算： $2 t a n 45 ° {(- \frac{1}{2})}^{0} + | \sqrt{3} - 1 |$ ．

(2)、化简： $(\frac{1}{x - 2} - \frac{1}{x + 2}) ÷ \frac{x}{x^{2} - 4}$ ．

查看试题解析
7. 计算： $(- 2023)^{0} + \sqrt{4} - 2 s i n 30 ° + | - 5 |$ .

查看试题解析

二、解答题

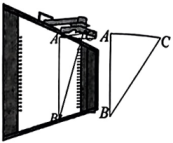8. 教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC， $∠ B A C = 90 °$ ．黑板上投影图像的高度 $A B = 120 c m$ ， CB与AB的夹角 $∠ B = 33.7 °$ ，求AC的长．（结果精确到1cm．参考数据： $s i n 33.7 ° \approx 0.55$ ， $c o s 33.7 ° \approx 0.83$ ， $t a n 33.7 ° \approx 0.67$ ）

查看试题解析
9. 如图所示是消防员攀爬云梯到小明家的场景．已知 $A E ⊥ B E ， B C ⊥ B E ， C D ∥ B E$ ， $A C = 10.4 m ， B C = 1.26 m$ ，点 $A$ 关于点 $C$ 的仰角为 $70 °$ ，则楼 $A E$ 的高度为多少 $m$ ？（结果保留整数．参考数据： $s i n 70 ° \approx 0.94 ， c o s 70 ° \approx 0.34 ， t a n 70 ° \approx 2.75$ ）

查看试题解析

10. 某实践探究小组想测得湖边两处的距离，数据勘测组通过勘测，得到了如下记录表：

实践探究活动记录表
活动内容测量湖边A、B两处的距离
成员组长：××× 组员：××××××××××××
测量工具测角仪，皮尺等
测量示意图		说明：因为湖边A、B两处的距离无法直接测量，数据勘测组在湖边找了一处位置C．可测量C处到A、B两处的距离．通过测角仪可测得 $∠ A 、 ∠ B 、 ∠ C$ 的度数．
测量数据	角的度数	$∠ A = 30 °$
		$∠ B = 45 °$
		$∠ C = 105 °$
	边的长度	$B C = 40.0$ 米
		$A C = 56.4$ 米

数据处理组得到上面数据以后做了认真分析．他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离．于是数据处理组写出了以下过程，请补全内容．

(1)、

已知：如图，在 $△ A B C$ 中， $∠ A = 30 ° ， ∠ B = 45 °$ ． ____．（从记录表中再选一个条件填入横线）

求：线段 $A B$ 的长．（为减小结果的误差，若有需要， $\sqrt{2}$ 取 $1.41$ ， $\sqrt{3}$ 取 $1.73$ ， $\sqrt{6}$ 取 $2.45$ 进行计算，最后结果保留整数．）

查看试题解析

11. 渝昆高速铁路的建成，将会显著提升宜宾的交通地位．渝昆高速铁路宜宾临港长江公铁两用大桥（如图 $1$ ），桥面采用国内首创的公铁平层设计．为测量左桥墩底到桥面的距离 $C D$ ，如图 $2$ ．在桥面上点 $A$ 处，测得 $A$ 到左桥墩 $D$ 的距离 $A D = 200$ 米，左桥墩所在塔顶 $B$ 的仰角 $∠ B A D = 45 °$ ，左桥墩底 $C$ 的俯角 $∠ C A D = 15 °$ ，求 $C D$ 的长度．（结果精确到 $1$ 米．参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
12. 渔湾是国家“AAAA”级风景区，图1是景区游览的部分示意图.如图2，小卓从九孔桥A处出发，沿着坡角为48°的山坡向上走了92m到达B处的三龙潭瀑布，再沿坡角为37°的山坡向上走了30m到达C处的二龙潭瀑布.求小卓从A处的九孔桥到C处的二龙潭瀑布上升的高度DC为多少米？（结果精确到0.1m）
（参考数据：sin48°≈0.74，cos48°≈0.67，sin37°≈0.60，cos37°≈0.80）

查看试题解析
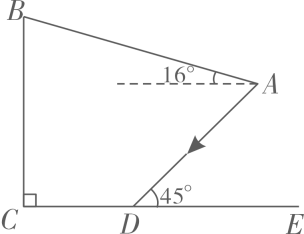
13. 为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装遮阳篷，便于社区居民休憩.
如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，当太阳光线AD与地面CE的夹角为45°时，求阴影CD的长.（结果精确到0.1米；参考数据： $s i n 16 ° ≈ 0.28$ ， $c o s 16 ° ≈ 0.96$ ， $t a n 16 ° ≈ 0.29$ ）

查看试题解析
14. 如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A-D-C．已知DC⊥BC，AB⊥BC．∠A=60°，AB=11m，CD=4m．求管道A-D-C的总长.

查看试题解析
15. 如图，某数学兴趣小组为了测量古树 $D E$ 的高度，采用了如下的方法：先从与古树底端 $D$ 在同一水平线上的点A出发，沿斜面坡度为 $i = 2 ： \sqrt{3}$ 的斜坡 $A B$ 前进 $20 \sqrt{7} m$ 到达点 $B$ ，再沿水平方向继续前进一段距离后到达点 $C$ ．在点 $C$ 处测得古树 $D E$ 的顶端 $E$ 的俯角为 $37 °$ ，底部 $D$ 的俯角为 $60 °$ ，求古树 $D E$ 的高度（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $c o s 37 ° \approx \frac{4}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ，计算结果用根号表示，不取近似值）．

查看试题解析

三、综合题

16. 鄂州市莲花山是国家4A级风景区，元明塔造型独特，是莲花山风景区的核心景点，深受全国各地旅游爱好者的青睐．今年端午节，景区将举行大型包粽子等节日庆祝活动．如图2，景区工作人员小明准备从元明塔的点G处挂一条大型竖直条幅到点E处，挂好后，小明进行实地测量，从元明塔底部F点沿水平方向步行30米到达自动扶梯底端A点，在A点用仪器测得条幅下端E的仰角为30°；接着他沿自动扶梯AD到达扶梯顶端D点，测得点A和点D的水平距离为15米，且tan∠DAB= $\frac{4}{3}$ ；然后他从D点又沿水平方向行走了45米到达C点，在C点测得条幅上端G的仰角为45°．（图上各点均在同一个平面内，且G，C，B共线，F，A，B共线，G、E、F共线，CD∥AB，GF⊥FB）．

(1)、求自动扶梯AD的长度；

(2)、求大型条幅GE的长度．（结果保留根号）

查看试题解析
17. 如图，直线 $M N$ 和 $E F$ 为河的两岸，且 $M N ∥ E F$ ，为了测量河两岸之间的距离，某同学在河岸 $F E$ 的B点测得 $∠ C B E = 30 °$ ，从B点沿河岸 $F E$ 的方向走40米到达D点，测得 $∠ C D E = 45 °$ .

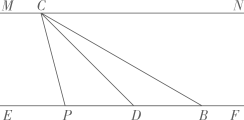(1)、求河两岸之间的距离是多少米？（结果保留根号）

(2)、若从D点继续沿 $D E$ 的方向走 $(12 \sqrt{3} + 12)$ 米到达P点.求 $t a n ∠ C P E$ 的值.

查看试题解析
18. “一缕清风银叶转”，某市20台风机依次矗立在云遮雾绕的山脊之上，风叶转动，风能就能转换成电能，造福千家万户．某中学初三数学兴趣小组，为测量风叶的长度进行了实地测量．如图，三片风叶两两所成的角为 $120 °$ ，当其中一片风叶 $O B$ 与塔干 $O D$ 叠合时，在与塔底D水平距离为60米的E处，测得塔顶部O的仰角 $∠ O E D = 45 °$ ，风叶 $O A$ 的视角 $∠ O E A = 30 °$ ．

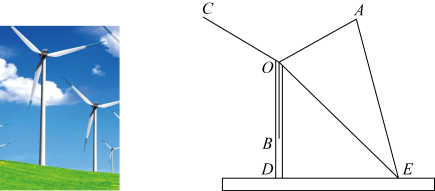(1)、已知α，β两角和的余弦公式为： $c o s (α + β) = c o s α c o s β - s i n α s i n β$ ，请利用公式计算 $c o s 75 °$ ；

(2)、求风叶 $O A$ 的长度．

查看试题解析
19. 某校学生开展综合实践活动，测量某建筑物的高度 $A B$ ，在建筑物附近有一斜坡，坡长 $C D = 10$ 米，坡角 $α = 30 °$ ，小华在C处测得建筑物顶端A的仰角为 $60 °$ ，在D处测得建筑物顶端A的仰角为 $30 °$ ．（已知点A，B，C，D在同一平面内，B，C在同一水平线上）

(1)、求点D到地面 $B C$ 的距离；

(2)、求该建筑物的高度 $A B$ ．

查看试题解析