2023年中考数学真题分类汇编(全国版):锐角三角函数(1)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 爬坡时坡角与水平面夹角为α,则每爬1m耗能 , 若某人爬了1000m,该坡角为30°,则他耗能( ).(参考数据: , )
 A、58J B、159J C、1025J D、1732J2. 的值等于( )A、1 B、 C、 D、23. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , )
A、58J B、159J C、1025J D、1732J2. 的值等于( )A、1 B、 C、 D、23. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , ) A、 B、 C、 D、4. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )
A、 B、 C、 D、4. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )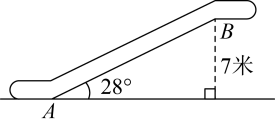 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( )
5. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( ) A、米 B、米 C、米 D、米6. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、87. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( )
A、米 B、米 C、米 D、米6. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、87. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( ) A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米二、填空题
-
8. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号)
 9. 为发展城乡经济,建设美丽乡村,某乡对地和地之间的一处垃圾填埋场进行改造,把原来地去往地需要绕行到地的路线,改造成可以直线通行的公路 . 如图,经勘测,千米, , , 则改造后公路的长是千米(精确到千米;参考数据: , , , ).
9. 为发展城乡经济,建设美丽乡村,某乡对地和地之间的一处垃圾填埋场进行改造,把原来地去往地需要绕行到地的路线,改造成可以直线通行的公路 . 如图,经勘测,千米, , , 则改造后公路的长是千米(精确到千米;参考数据: , , , ). 10. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)
10. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)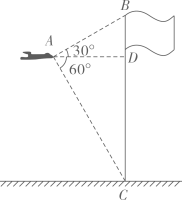
三、计算题
-
11. 计算: .12.(1)、化简:;(2)、先化简,再求值: , 其中 .13.(1)、计算:;(2)、先化简,再求值: , 化简后,从的范围内选择一个你喜欢的整数作为x的值代入求值.14. 先化简,再求值: , 其中 .15. 计算:16. 计算: .17.(1)、计算:(2)、分解因式:
四、解答题
-
18. 如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”.“兰州龙源”的“龙”字主题雕塑以紫铜铸造,如巨龙腾空,气势如虹,屹立在黄河北岸.某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动.具体过程如下:如图2,“龙”字雕塑CD位于垂直地面的基座BC上,在平行于水平地面的A处测得、 , . 求“龙”字雕塑的高度.(B,C,D三点共线, . 结果精确到0.1m)(参考数据: , , , , , )

 19. 徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点处,用测角仪测得塔顶的仰角 , 他在平地上沿正对电视塔的方向后退至点处,测得塔顶的仰角 . 若测角仪距地面的高度 , 求电视塔的高度(精确到 . (参考数据:)
19. 徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点处,用测角仪测得塔顶的仰角 , 他在平地上沿正对电视塔的方向后退至点处,测得塔顶的仰角 . 若测角仪距地面的高度 , 求电视塔的高度(精确到 . (参考数据:)
 20. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形 , 斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米, , 求斜坡的长.(结果精确到米)(参考数据:)
20. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形 , 斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米, , 求斜坡的长.(结果精确到米)(参考数据:) 21. 一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯灯杆底部不可到达的高如图所示,当小明爸爸站在点处时,他在该景观灯照射下的影子长为 , 测得;当小明站在爸爸影子的顶端处时,测得点的仰角为已知爸爸的身高 , 小明眼睛到地面的距离 , 点、、在同一条直线上, , , 求该景观灯的高参考数据: , ,
21. 一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯灯杆底部不可到达的高如图所示,当小明爸爸站在点处时,他在该景观灯照射下的影子长为 , 测得;当小明站在爸爸影子的顶端处时,测得点的仰角为已知爸爸的身高 , 小明眼睛到地面的距离 , 点、、在同一条直线上, , , 求该景观灯的高参考数据: , , 22. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据: , . 结果精确到).
22. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据: , . 结果精确到). 23. 先化简,再求值: , 其中满足 .24. 我国航天事业捷报频传,2023年5月30日,被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功,如图(九),有一枚运载火箭从地面处发射,当火箭到达处时,地面处的雷达站测得距离是 , 仰角为 . , 火箭直线到达处,此时地面处雷达站测得处的仰角为 . 求火箭从到处的平均速度(结果精确到).(参考数据:)
23. 先化简,再求值: , 其中满足 .24. 我国航天事业捷报频传,2023年5月30日,被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功,如图(九),有一枚运载火箭从地面处发射,当火箭到达处时,地面处的雷达站测得距离是 , 仰角为 . , 火箭直线到达处,此时地面处雷达站测得处的仰角为 . 求火箭从到处的平均速度(结果精确到).(参考数据:)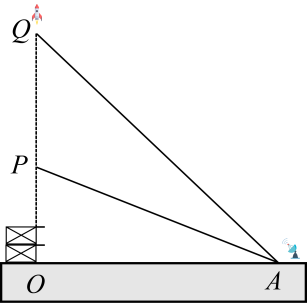
五、综合题
-
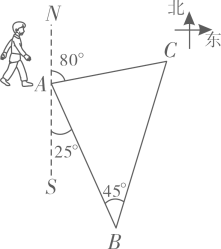
25. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.
⑴求行进路线BC和CA所在直线的夹角的度数;
⑵求检查点和之间的距离(结果保留根号).
 26. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)
26. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上) (1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).
(1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).(参考数据: , , , )