2023年中考数学真题分类汇编(全国版):图形的相似
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 若 , 则( )A、6 B、 C、1 D、2. 若两个相似三角形周长的比为 , 则这两个三角形对应边的比是( )A、 B、 C、 D、3. 如图,已知 , , 若的长度为6,则的长度为( )
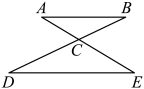 A、4 B、9 C、12 D、4. 常言道:失之毫厘,谬以千里.当人们向太空发射火箭或者描述星际位置时,需要非常准确的数据.的角真的很小.把整个圆等分成360份,每份这样的弧所对的圆心角的度数是 . . 若一个等腰三角形的腰长为1千米,底边长为4.848毫米,则其顶角的度数就是 . 太阳到地球的平均距离大约为千米.若以太阳到地球的平均距离为腰长,则顶角为的等腰三角形底边长为( )A、24.24千米 B、72.72千米 C、242.4千米 D、727.2千米5. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( )
A、4 B、9 C、12 D、4. 常言道:失之毫厘,谬以千里.当人们向太空发射火箭或者描述星际位置时,需要非常准确的数据.的角真的很小.把整个圆等分成360份,每份这样的弧所对的圆心角的度数是 . . 若一个等腰三角形的腰长为1千米,底边长为4.848毫米,则其顶角的度数就是 . 太阳到地球的平均距离大约为千米.若以太阳到地球的平均距离为腰长,则顶角为的等腰三角形底边长为( )A、24.24千米 B、72.72千米 C、242.4千米 D、727.2千米5. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( ) A、 B、 C、 D、6. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数7. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( )
A、 B、 C、 D、6. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数7. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( ) A、 B、 C、 D、8. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
A、 B、 C、 D、8. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( ) A、 B、 C、 D、9. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )
A、 B、 C、 D、9. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 如图,一束光线从点出发,经过y轴上的点反射后经过点 , 则的值是 .
 11. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 .
11. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 . 12. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)
12. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)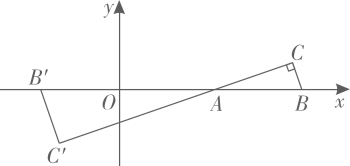 13. 如图,乐器上的一根弦 , 两个端点固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,之间的距离为 .
13. 如图,乐器上的一根弦 , 两个端点固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,之间的距离为 .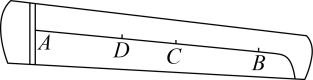 14. 小慧同学在学习了九年级上册“4.1比例线段”3节课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值+感受这种特殊化的学习过程.
14. 小慧同学在学习了九年级上册“4.1比例线段”3节课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值+感受这种特殊化的学习过程.
三、解答题
-
15. 综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪ABCD为正方形,AB=30cm,顶点A处挂了一个铅锤M.如图是测量树高的示意图,测高仪上的点D,A与树顶E在一条直线上,铅垂线AM交BC于点H.经测量,点A距地面1.8m,到树EC的距离m,cm.求树EG的高度(结果精确到0.1m).

四、综合题
-
16. 阅读下列材料,回答问题
任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大度远大于南北走向的最大宽度,如图1.
工具:一把皮尺(测量长度略小于)和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度);测角仪的功能是测量角的大小,即在任一点处,对其视线可及的两点,可测得的大小,如图3.

小明利用皮尺测量,求出了小水池的最大宽度 , 其测量及求解过程如下:测量过程:
(ⅰ)在小水池外选点 , 如图4,测得;
(ⅱ)分别在上测得;测得 . 求解过程:
由测量知, ,
, 又①____,
.
又②____( .
故小水池的最大宽度为____ .
(1)、补全小明求解过程中①②所缺的内容;(2)、小明求得用到的几何知识是;(3)、小明仅利用皮尺,通过5次测量,求得 . 请你同时利用皮尺和测角仪,通过测量长度、角度等几何量,并利用解直角三角形的知识求小水池的最大宽度 , 写出你的测量及求解过程.要求:测量得到的长度用字母表示,角度用表示;测量次数不超过4次(测量的几何量能求出 , 且测量的次数最少,才能得满分).
17. 如图,在正方形中,E,F分别是边 , 上的点,连接 , , . (1)、若正方形的边长为2,E是的中点.
(1)、若正方形的边长为2,E是的中点.①如图1,当时,求证:;
②如图2,当时,求的长;
(2)、如图3,延长 , 交于点G,当时,求证: .
-