2023年中考数学真题分类汇编(全国版):圆(3)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在中,半径互相垂直,点在劣弧上.若 , 则( )
 A、 B、 C、 D、2. 圆心角为 , 半径为3的扇形弧长为( )A、 B、 C、 D、3. 如图1是一段弯管,弯管的部分外轮廓线如图2所示是一条圆弧 , 圆弧的半径 , 圆心角 , 则( )
A、 B、 C、 D、2. 圆心角为 , 半径为3的扇形弧长为( )A、 B、 C、 D、3. 如图1是一段弯管,弯管的部分外轮廓线如图2所示是一条圆弧 , 圆弧的半径 , 圆心角 , 则( ) A、 B、 C、 D、4. 一个几何体的三视图如下,则这个几何体的表面积是( )
A、 B、 C、 D、4. 一个几何体的三视图如下,则这个几何体的表面积是( ) A、 B、 C、 D、5. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )
A、 B、 C、 D、5. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )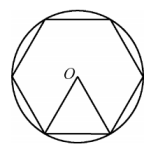 A、 B、 C、3 D、6. 如图,内接于 , 是的直径,连接 , , 则的度数是( )
A、 B、 C、3 D、6. 如图,内接于 , 是的直径,连接 , , 则的度数是( )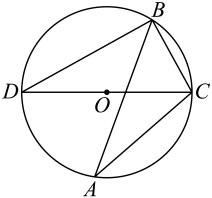 A、 B、 C、 D、7. 如图,正六边形内接于 , 点P在上,Q是的中点,则的度数为( )
A、 B、 C、 D、7. 如图,正六边形内接于 , 点P在上,Q是的中点,则的度数为( )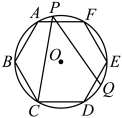 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图,是的直径,切于点A,交于点 , 连接 , 若 , 则 .
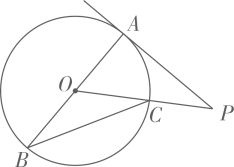 9. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角 , 则该圆锥的底面圆的半径r长为 .
9. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角 , 则该圆锥的底面圆的半径r长为 . 10. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .11. 以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转°.
10. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .11. 以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转°. 12. 如图,小珍同学用半径为 , 圆心角为的扇形纸片,制作一个底面半径为的圆锥侧面,则圆锥上粘贴部分的面积是 .
12. 如图,小珍同学用半径为 , 圆心角为的扇形纸片,制作一个底面半径为的圆锥侧面,则圆锥上粘贴部分的面积是 . 13. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .
13. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .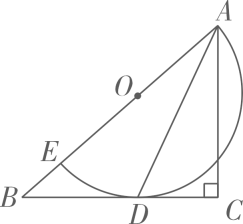
三、综合题
-
14. 如图,AB为⊙O的直径,E为⊙O上一点,点C为的中点,过点C作CD⊥AE,交AE的延长线于点D,延长DC交AB的延长线于点F.
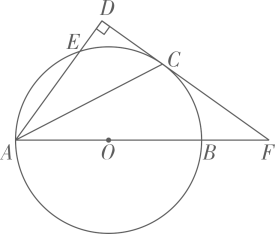 (1)、求证:CD是⊙O的切线;(2)、若DE=1,DC=2,求⊙的半径长.15. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , .
(1)、求证:CD是⊙O的切线;(2)、若DE=1,DC=2,求⊙的半径长.15. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , . (1)、求证:是切线;(2)、若 , , 求的长.16. 如图,是的外接圆,是的直径,是延长线上一点,连接 , 且.
(1)、求证:是切线;(2)、若 , , 求的长.16. 如图,是的外接圆,是的直径,是延长线上一点,连接 , 且. (1)、求证:是的切线;(2)、若直径 , 求的长.17. 在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请应用此结论.解决以下问题:
(1)、求证:是的切线;(2)、若直径 , 求的长.17. 在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请应用此结论.解决以下问题:如图1,中,().点D是边上的一动点(点D不与B,C重合),将线段绕点A顺时针旋转到线段 , 连接 .
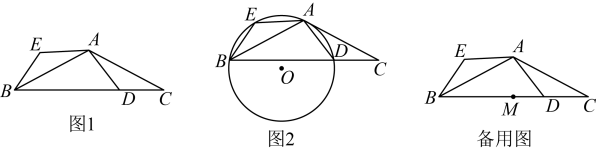 (1)、求证:A,E,B,D四点共圆;(2)、如图2,当时,是四边形的外接圆,求证:是的切线;(3)、已知 , 点M是边的中点,此时是四边形的外接圆,直接写出圆心P与点M距离的最小值.18. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .
(1)、求证:A,E,B,D四点共圆;(2)、如图2,当时,是四边形的外接圆,求证:是的切线;(3)、已知 , 点M是边的中点,此时是四边形的外接圆,直接写出圆心P与点M距离的最小值.18. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .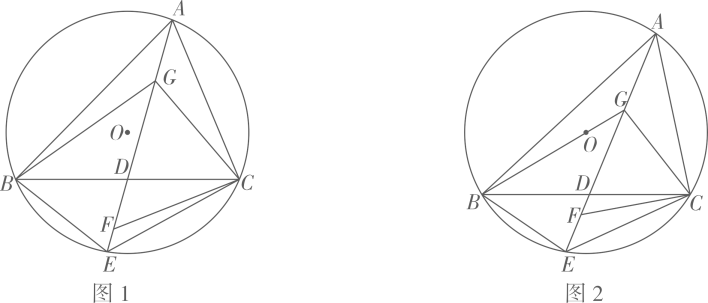 (1)、求的度数.(2)、①求证: .
(1)、求的度数.(2)、①求证: .②若 , 求的值,
(3)、如图2,当点O恰好在上且时,求的长.19. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H. (1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.
(1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.下面三个问题,依次按照易、中、难排列,对应的分值为2分、3分、4分,请根据自己的认知水平,选择其中一道问题进行解答。
①若OF= , 求BC的长;
②若AH= , 求△ANB的局长:
③若HF·AB=88.求△BHC的面积.