2023年中考数学真题分类汇编(全国版):圆(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在中,若 , , 则扇形(阴影部分)的面积是( )
 A、 B、 C、 D、2. 为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为 , 大圆半径为 , 每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )
A、 B、 C、 D、2. 为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为 , 大圆半径为 , 每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )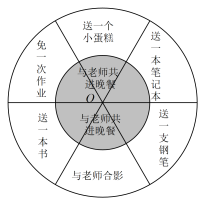 A、 B、 C、 D、3. 如图,已知点在上,为的中点.若 , 则等于( )
A、 B、 C、 D、3. 如图,已知点在上,为的中点.若 , 则等于( ) A、 B、 C、 D、4. 如图,在中, , 则( )
A、 B、 C、 D、4. 如图,在中, , 则( ) A、1 B、2 C、 D、45. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )
A、1 B、2 C、 D、45. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )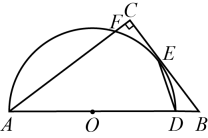 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
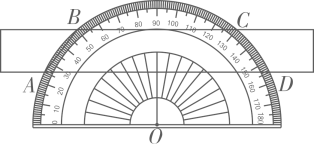
6. 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接 , 则的度数为 .
 7. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留)
7. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留) 8. 若扇形的圆心角为 , 半径为18,则它的弧长为。9. 如图,四边形内接于圆 , 若 , 则的度数是.
8. 若扇形的圆心角为 , 半径为18,则它的弧长为。9. 如图,四边形内接于圆 , 若 , 则的度数是. 10. 用半径为 , 面积为的扇形纸片,围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .11. 如图,圆锥形烟囱帽的底面半径为 , 母线长为 , 则烟囱帽的侧面积为 . (结果保留)
10. 用半径为 , 面积为的扇形纸片,围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .11. 如图,圆锥形烟囱帽的底面半径为 , 母线长为 , 则烟囱帽的侧面积为 . (结果保留) 12. 图1是方格绘成的七巧板图案,每个小方格的边长为 , 现将它前拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为.若点A,N,M在同一直线上, , 则题字区域的面积为.
12. 图1是方格绘成的七巧板图案,每个小方格的边长为 , 现将它前拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为.若点A,N,M在同一直线上, , 则题字区域的面积为.
三、作图题
-
13. 如图,在中, , 以为直径的交边于点 , 连接 , 过点作.
 (1)、请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)(2)、在(1)的条件下,求证:.
(1)、请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)(2)、在(1)的条件下,求证:.四、综合题
-
14. 如图,为的直径,点C是的中点,过点C做射线的垂线,垂足为E.
 (1)、求证:是切线;(2)、若 , 求的长;(3)、在(2)的条件下,求阴影部分的面积(用含有的式子表示).15. 如图,是的内接三角形,是的直径, , 点在上,连接并延长,交于点 , 连接 , 作 , 垂足为 .
(1)、求证:是切线;(2)、若 , 求的长;(3)、在(2)的条件下,求阴影部分的面积(用含有的式子表示).15. 如图,是的内接三角形,是的直径, , 点在上,连接并延长,交于点 , 连接 , 作 , 垂足为 .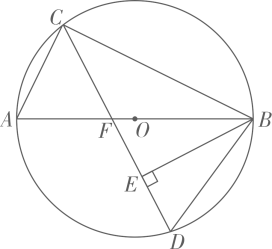 (1)、求证:;(2)、若 , 求的长.16. 在中,半径垂直于弦 , 垂足为D, , E为弦所对的优弧上一点.
(1)、求证:;(2)、若 , 求的长.16. 在中,半径垂直于弦 , 垂足为D, , E为弦所对的优弧上一点.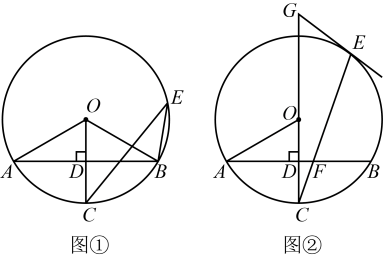 (1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.17. 如图,是的直径,点 , 是上的点,且 , 连接 , 过点作的垂线,交的延长线于点 , 交的延长线于点 , 过点作于点 , 交于点 .
(1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.17. 如图,是的直径,点 , 是上的点,且 , 连接 , 过点作的垂线,交的延长线于点 , 交的延长线于点 , 过点作于点 , 交于点 . (1)、求证:是的切线;(2)、若 , , 求的长.18. 如图,是的直径,点是外一点,与相切于点 , 点为上的一点.连接、、 , 且 .
(1)、求证:是的切线;(2)、若 , , 求的长.18. 如图,是的直径,点是外一点,与相切于点 , 点为上的一点.连接、、 , 且 . (1)、求证:为的切线;(2)、延长与的延长线交于点D,求证:;(3)、若 , 求阴影部分的面积.19. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设.
(1)、求证:为的切线;(2)、延长与的延长线交于点D,求证:;(3)、若 , 求阴影部分的面积.19. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设. (1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.20. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
(1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.20. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D. (1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.
(1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.
-