2023年中考数学真题分类汇编(全国版):圆(1)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
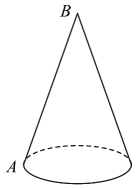
1. 某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 , 母线长为30 , 为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
v
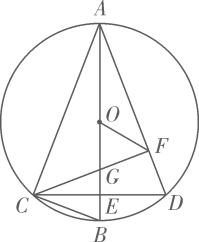
 A、 B、 C、 D、2. 如果圆锥侧面展开图的面积是 , 母线长是 , 则这个圆锥的底面半径是( )A、3 B、4 C、5 D、63. 如图,圆内接四边形中, , 连接 , , , , . 则的度数是( )
A、 B、 C、 D、2. 如果圆锥侧面展开图的面积是 , 母线长是 , 则这个圆锥的底面半径是( )A、3 B、4 C、5 D、63. 如图,圆内接四边形中, , 连接 , , , , . 则的度数是( ) A、 B、 C、 D、4. 如图,点A,B,C在上,若 , 则的度数为( )
A、 B、 C、 D、4. 如图,点A,B,C在上,若 , 则的度数为( ) A、95° B、100° C、105° D、110°5. 如图,是的直径, , 则( )
A、95° B、100° C、105° D、110°5. 如图,是的直径, , 则( ) A、 B、 C、 D、6. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( )
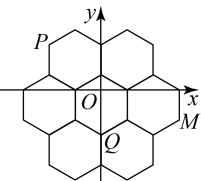
A、 B、 C、 D、6. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( ) A、 B、 C、 D、7. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
A、 B、 C、 D、7. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图,在中,为直径,C为圆上一点,的角平分线与交于点D,若 , 则°.
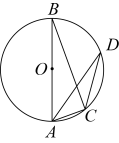 9. 如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心,半径r为 , 点A,B是圆上的两点,圆心角 , 则的长为 . (结果保留)
9. 如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心,半径r为 , 点A,B是圆上的两点,圆心角 , 则的长为 . (结果保留) 10. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是 , 为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器台.
10. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是 , 为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器台.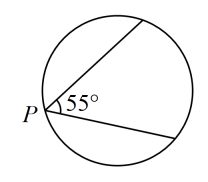 11. 如图,分别与相切于两点,且 . 若点是上异于点的一点,则的大小为 .
11. 如图,分别与相切于两点,且 . 若点是上异于点的一点,则的大小为 . 12. 如图,某数学兴趣小组用一张半径为的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为 , 那么这张扇形纸板的面积为 . (结果保留)
12. 如图,某数学兴趣小组用一张半径为的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为 , 那么这张扇形纸板的面积为 . (结果保留) 13. 如图,在中, , 则的度数为 .
13. 如图,在中, , 则的度数为 .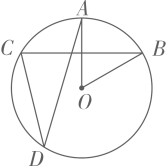 14. 若正多边形的一个内角等于 , 则这个正多边形的边数是 .
14. 若正多边形的一个内角等于 , 则这个正多边形的边数是 .三、作图题
-
15. 已知:点P是外一点.
 (1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.
(1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.四、综合题
-
16. 如图,AB是的直径,AC是弦,是上一点,是AB延长线上一点,连接AD,DC,CP.
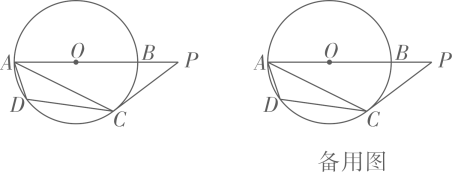 (1)、求证:∠ADC-∠BAC=90°;(请用两种证法解答)(2)、 , 的半径为 , 求AP的长.17. 如图,在中, , 点在上,以为圆心,为半径的半圆分别交 , 于点 , 且点是弧的中点.
(1)、求证:∠ADC-∠BAC=90°;(请用两种证法解答)(2)、 , 的半径为 , 求AP的长.17. 如图,在中, , 点在上,以为圆心,为半径的半圆分别交 , 于点 , 且点是弧的中点. (1)、求证:是的切线;(2)、若 , 求图中阴影部分的面积(结果保留).18. 如图,是的直径,点E,C在上,点C是的中点,垂直于过C点的直线 , 垂足为D,的延长线交直线于点F.
(1)、求证:是的切线;(2)、若 , 求图中阴影部分的面积(结果保留).18. 如图,是的直径,点E,C在上,点C是的中点,垂直于过C点的直线 , 垂足为D,的延长线交直线于点F.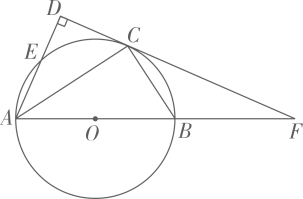 (1)、求证:是的切线;(2)、若 , , ①求的半径;②求线段的长.19. 2023年5月30日,“神舟十六号”航天飞船成功发射.如图,飞船在离地球大约的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在中, .
(1)、求证:是的切线;(2)、若 , , ①求的半径;②求线段的长.19. 2023年5月30日,“神舟十六号”航天飞船成功发射.如图,飞船在离地球大约的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在中, .(参考数据:)
 (1)、求的值(精确到);(2)、在中,求的长(结果取整数).20. 综合探究
(1)、求的值(精确到);(2)、在中,求的长(结果取整数).20. 综合探究如图1,在矩形中 , 对角线相交于点 , 点关于的对称点为 , 连接交于点 , 连接 .
 (1)、求证:;(2)、以点为圆心,为半径作圆.
(1)、求证:;(2)、以点为圆心,为半径作圆.①如图2,与相切,求证:;
②如图3,与相切, , 求的面积.
-