2023年中考数学真题分类汇编(全国版):四边形(3)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 面积为9的正方形,其边长等于( )A、9的平方根 B、9的算术平方根 C、9的立方根 D、5的算术平方根2. 若一个菱形的两条对角线长分别是关于的一元二次方程的两个实数根,且其面积为11,则该菱形的边长为( )A、 B、 C、 D、3. 如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是中点,若 , , 则的长为( )
 A、1 B、2 C、3 D、44. 如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角( )
A、1 B、2 C、3 D、44. 如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角( ) A、 B、 C、 D、5. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A、 B、 C、 D、5. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( ) A、 B、 C、 D、6. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
A、 B、 C、 D、6. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )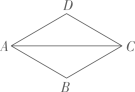 A、 B、1 C、 D、7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
A、 B、1 C、 D、7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤二、填空题
-
8. 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 个.
 9. 如图,把两根钢条OA,OB的一个端点连在一起,点C,D分别是OA,OB的中点.若CD=4cm,则该工件内槽宽AB的长为cm.
9. 如图,把两根钢条OA,OB的一个端点连在一起,点C,D分别是OA,OB的中点.若CD=4cm,则该工件内槽宽AB的长为cm.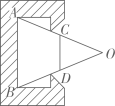 10. 如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕 , 小宇测得长边 , 则四边形的周长为 .
10. 如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕 , 小宇测得长边 , 则四边形的周长为 . 11. 如图,在正方形中,对角线与相交于点O,E为上一点, , F为的中点,若的周长为32,则的长为 .
11. 如图,在正方形中,对角线与相交于点O,E为上一点, , F为的中点,若的周长为32,则的长为 . 12. 如图,在中, , 垂足为 . 以点为圆心,长为半径画弧,与分别交于点 . 若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为 , 则 . (结果保留根号)
12. 如图,在中, , 垂足为 . 以点为圆心,长为半径画弧,与分别交于点 . 若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为 , 则 . (结果保留根号)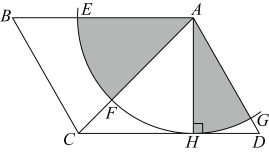 13. 如果一个多边形每一个外角都是 , 那么这个多边形的边数为 .14. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。
13. 如果一个多边形每一个外角都是 , 那么这个多边形的边数为 .14. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。 15. 如图,的顶点的坐标分别是 . 则顶点的坐标是 .
15. 如图,的顶点的坐标分别是 . 则顶点的坐标是 . 16. 如图, , 是正方形的边的三等分点,是对角线上的动点,当取得最小值时,的值是 .
16. 如图, , 是正方形的边的三等分点,是对角线上的动点,当取得最小值时,的值是 . 17. 若七边形的内角中有一个角为 , 则其余六个内角之和为 .18. 如图,分别以a,b,m,n为边长作正方形,已知m>n且满足am-bn=2.an+bm=4.
17. 若七边形的内角中有一个角为 , 则其余六个内角之和为 .18. 如图,分别以a,b,m,n为边长作正方形,已知m>n且满足am-bn=2.an+bm=4. (1)、若a=3,b=4,则图1阴影部分的面积是;(2)、若图1阴影部分的面积为3.图2四边形ABCD的面积为5,则图2阴影部分的面积是 。19. 如图,在中, , , , 点是上一动点,将沿折叠得到 , 当点恰好落在上时,的长为 .
(1)、若a=3,b=4,则图1阴影部分的面积是;(2)、若图1阴影部分的面积为3.图2四边形ABCD的面积为5,则图2阴影部分的面积是 。19. 如图,在中, , , , 点是上一动点,将沿折叠得到 , 当点恰好落在上时,的长为 .
三、解答题
-
20. 莲花湖湿地公园是当地人民喜爱的休闲景区之一,里面的秋千深受孩子们喜爱.如图所示,秋千链子的长度为 , 当摆角恰为时,座板离地面的高度为 , 当摆动至最高位置时,摆角为 , 求座板距地面的最大高度为多少?(结果精确到;参考数据: , , , , , )
 21. 如图,在平行四边形中,点、分别在边和上,且 . 求证: .
21. 如图,在平行四边形中,点、分别在边和上,且 . 求证: .
四、综合题
-
22. 为了美化环境,提高民众的生活质量,市政府在三角形花园边上修建一个四边形人工湖泊 , 并沿湖泊修建了人行步道.如图,点在点的正东方向170米处,点在点的正北方向,点都在点的正北方向,长为100米,点在点的北偏东方向,点在点的北偏东方向.
 (1)、求步道的长度.(2)、点处有一个小商店,某人从点出发沿人行步道去商店购物,可以经点到达点 , 也可以经点到达点 , 请通过计算说明他走哪条路较近.结果精确到个位)(参考数据:)23. 定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角.
(1)、求步道的长度.(2)、点处有一个小商店,某人从点出发沿人行步道去商店购物,可以经点到达点 , 也可以经点到达点 , 请通过计算说明他走哪条路较近.结果精确到个位)(参考数据:)23. 定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角. (1)、如图1,在四边形中, , 对角线平分 . 求证:四边形为邻等四边形.(2)、如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.(3)、如图3,四边形是邻等四边形, , 为邻等角,连接 , 过B作交的延长线于点E.若 , 求四边形的周长.24. 超速容易造成交通事故.高速公路管理部门在某隧道内的两处安装了测速仪,该段隧道的截面示意图如图所示,图中所有点都在同一平面内,且在同一直线上.点、点到的距离分别为 , 且 , 在处测得点的俯角为 , 在处测得点的俯角为 , 小型汽车从点行驶到点所用时间为 .
(1)、如图1,在四边形中, , 对角线平分 . 求证:四边形为邻等四边形.(2)、如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.(3)、如图3,四边形是邻等四边形, , 为邻等角,连接 , 过B作交的延长线于点E.若 , 求四边形的周长.24. 超速容易造成交通事故.高速公路管理部门在某隧道内的两处安装了测速仪,该段隧道的截面示意图如图所示,图中所有点都在同一平面内,且在同一直线上.点、点到的距离分别为 , 且 , 在处测得点的俯角为 , 在处测得点的俯角为 , 小型汽车从点行驶到点所用时间为 . (1)、求两点之间的距离(结果精确到);(2)、若该隧道限速80千米/小时,判断小型汽车从点行驶到点是否超速?并通过计算说明理由.(参考数据:)25. 如图,四边形是边长为的菱形, , 点为的中点,为线段上的动点,现将四边形沿翻折得到四边形 .
(1)、求两点之间的距离(结果精确到);(2)、若该隧道限速80千米/小时,判断小型汽车从点行驶到点是否超速?并通过计算说明理由.(参考数据:)25. 如图,四边形是边长为的菱形, , 点为的中点,为线段上的动点,现将四边形沿翻折得到四边形 . (1)、当时,求四边形的面积;(2)、当点在线段上移动时,设 , 四边形的面积为 , 求关于的函数表达式.26. 如图,在平面直角坐标系中,四边形是矩形,反比例函数的图象分别与交于点和点 , 且点为的中点.
(1)、当时,求四边形的面积;(2)、当点在线段上移动时,设 , 四边形的面积为 , 求关于的函数表达式.26. 如图,在平面直角坐标系中,四边形是矩形,反比例函数的图象分别与交于点和点 , 且点为的中点. (1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.27. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且.
(1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.27. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且. (1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.
(1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.①如图2,当点落在射线上时,求的长.
②当当是直角三角形时,求的长.
28.(1)、【问题情境 建构函数】如图1,在矩形中,是的中点, , 垂足为.设 , 试用含的代数式表示.
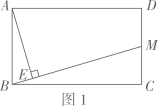 (2)、【由数想形 新知初探】
(2)、【由数想形 新知初探】在上述表达式中,与成函数关系,其图像如图2所示.若取任意实数,此时的函数图象是否具有对称性?若有,请说明理由,并在图2上补全函数图象.
 (3)、【数形结合 深度探究】
(3)、【数形结合 深度探究】在“取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值随的增大而增大;②函数值的取值范围是;③存在一条直线与该函数图象有四个交点;④在图像上存在四点 , 使得四边形是平行四边形.其中正确的是.(写出所有正确结论的序号)
(4)、【抽象回归 扩展总结】若将(1)中的“AB=4”改成“”,此时关于的函数表达式是 .一般地,当取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).