2023年中考数学真题分类汇编(全国版):四边形(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
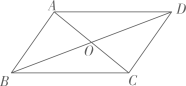 A、 B、 C、 D、2. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为 , 曲线终点为 , 过点的两条切线相交于点 , 列车在从到行驶的过程中转角为 . 若圆曲线的半径 , 则这段圆曲线的长为( ).
A、 B、 C、 D、2. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为 , 曲线终点为 , 过点的两条切线相交于点 , 列车在从到行驶的过程中转角为 . 若圆曲线的半径 , 则这段圆曲线的长为( ).
 A、 B、 C、 D、3. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )
A、 B、 C、 D、3. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )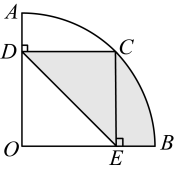 A、 B、 C、 D、4. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( )
A、 B、 C、 D、4. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( ) A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变5. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变5. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( ) A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD6. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )
A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD6. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )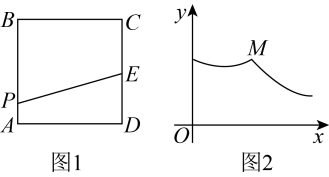 A、 B、 C、 D、7. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( )
A、 B、 C、 D、7. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( ) A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形
A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形二、填空题
-
8. 如图,在四边形ABCD中, , 于点O.请添加一个条件: , 使四边形ABCD成为菱形.
 9. 点是菱形的对称中心, , 连接 , 则的度数为 .10. 一块面积为的正方形桌布,其边长为 .11. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
9. 点是菱形的对称中心, , 连接 , 则的度数为 .10. 一块面积为的正方形桌布,其边长为 .11. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 . 12. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
12. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 . 13. 如图,在中,为的中点,过点且分别交于点 . 若 , 则的长为 .
13. 如图,在中,为的中点,过点且分别交于点 . 若 , 则的长为 .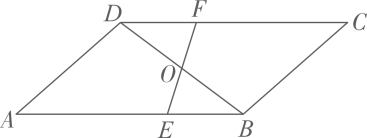 14. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 .
14. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 . 15. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm
15. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm(结果精确到0.1cm,参考数据: , , )
 16. 矩形纸片ABCD中, , , 点M在AD边所在的直线上,且 , 将矩形纸片ABCD折叠,使点B与点M重合,折痕与AD,BC分别交于点E,F,则线段EF的长度为.17. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
16. 矩形纸片ABCD中, , , 点M在AD边所在的直线上,且 , 将矩形纸片ABCD折叠,使点B与点M重合,折痕与AD,BC分别交于点E,F,则线段EF的长度为.17. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
三、解答题
-
18. 东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B在角楼A的正东方向处,南关桥C在城门楼B的正南方向处.在明珠大剧院P测得角楼A在北偏东方向,南关桥C在南偏东方向(点A,B,C,P四点在同一平面内).求明珠大剧院到龙堤的距离(结果精确到).
(参考数据: , , , , , )
 19. 某中学依山而建,校门A处有一坡角的斜坡 , 长度为30米,在坡顶B处测得教学楼的楼顶C的仰角 , 离B点4米远的E处有一个花台,在E处测得C的仰角 , 的延长线交水平线于点D,求的长(结果保留根号).
19. 某中学依山而建,校门A处有一坡角的斜坡 , 长度为30米,在坡顶B处测得教学楼的楼顶C的仰角 , 离B点4米远的E处有一个花台,在E处测得C的仰角 , 的延长线交水平线于点D,求的长(结果保留根号).
四、作图题
-
20. 如图,将边长为4的等边三角形纸片沿边上的高剪成两个三角形,用这两个三角形拼成一个平行四边形.
 (1)、画出这个平行四边形(画出一种情况即可);(2)、根据(1)中所画平行四边形求出两条对角线长.
(1)、画出这个平行四边形(画出一种情况即可);(2)、根据(1)中所画平行四边形求出两条对角线长.五、综合题
-
21. 如图,矩形的对角线 , 相交于点O, .
 (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.22. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , 交于点 , 探究与的数量关系.
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.22. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , 交于点 , 探究与的数量关系.
 (1)、问题探究:
(1)、问题探究:
先将问题特殊化,如图(2),当时,直接写出的大小;(2)、再探究一般情形,如图(1),求与的数量关系.问题拓展:
(3)、将图(1)特殊化,如图(3),当时,若 , 求的值.23. 如图,平行四边形的对角线相交于点 , 点在对角线上,且 , 连接 , . (1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.24. 综合与实践活动中,要利用测角仪测量塔的高度.
(1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.24. 综合与实践活动中,要利用测角仪测量塔的高度.如图,塔前有一座高为的观景台,已知 , 点E,C,A在同一条水平直线上.
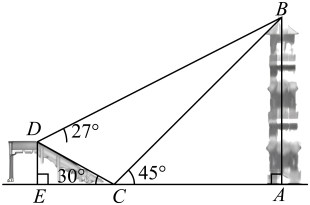
某学习小组在观景台C处测得塔顶部B的仰角为 , 在观景台D处测得塔顶部B的仰角为 .
(1)、求的长;(2)、设塔的高度为h(单位:m).①用含有h的式子表示线段的长(结果保留根号);
②求塔的高度(取0.5,取1.7,结果取整数).
25. 如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.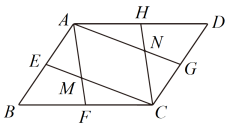 (1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.26. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.
(1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.26. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.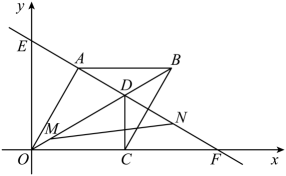 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.27.(1)、[问题探究]
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.27.(1)、[问题探究]如图1,在正方形中,对角线相交于点O.在线段上任取一点P(端点除外),连接 .
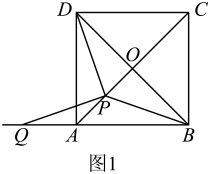
①求证:;
②将线段绕点P逆时针旋转,使点D落在的延长线上的点Q处.当点P在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系,并说明理由.
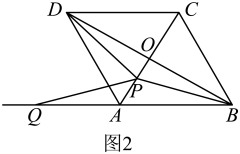
(2)、[迁移探究]如图2,将正方形换成菱形 , 且 , 其他条件不变.试探究与的数量关系,并说明理由.
 28. 在平面直角坐标系中,O为原点,菱形的顶点 , 矩形的顶点 .
28. 在平面直角坐标系中,O为原点,菱形的顶点 , 矩形的顶点 .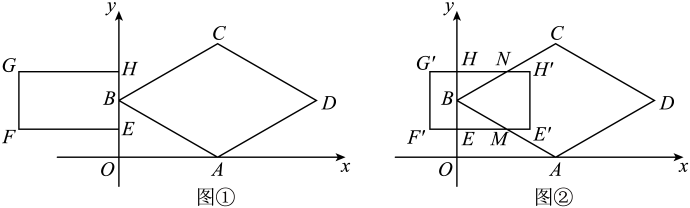 (1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.
(1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.①如图②,当边与相交于点M、边与相交于点N,且矩形与菱形重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当时,求S的取值范围(直接写出结果即可).
-