2023年中考数学真题分类汇编(全国版):四边形(1)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在平行四边形中, , , 将线段水平向右平移a个单位长度得到线段 , 若四边形为菱形时,则a的值为( )
 A、1 B、2 C、3 D、42. 下列命题正确的是( )A、正方形的对角线相等且互相平分 B、对角互补的四边形是平行四边形 C、矩形的对角线互相垂直 D、一组邻边相等的四边形是菱形3. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( )
A、1 B、2 C、3 D、42. 下列命题正确的是( )A、正方形的对角线相等且互相平分 B、对角互补的四边形是平行四边形 C、矩形的对角线互相垂直 D、一组邻边相等的四边形是菱形3. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( ) A、8 B、4 C、3.5 D、34. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( )
A、8 B、4 C、3.5 D、34. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、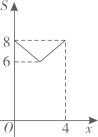 D、
D、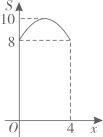 5. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( )
5. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( ) A、 B、 C、 D、6. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )
A、 B、 C、 D、6. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )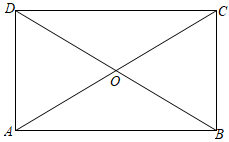 A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴7. 一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知 , 点D为边的中点,点A、B对应的刻度为1、7,则( )
A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴7. 一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知 , 点D为边的中点,点A、B对应的刻度为1、7,则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 若正n边形的一个外角为 , 则 .9. 如图,在矩形中对角线 , 交于点 , 请添加一个条件 , 使矩形是正方形(填一个即可)
 10. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 .
10. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 . 11. 如图,将面积为7的正方形和面积为9的正方形分别绕原点O顺时针旋转,使 , 落在数轴上,点A,D在数轴上对应的数字分别为a,b,则 .
11. 如图,将面积为7的正方形和面积为9的正方形分别绕原点O顺时针旋转,使 , 落在数轴上,点A,D在数轴上对应的数字分别为a,b,则 .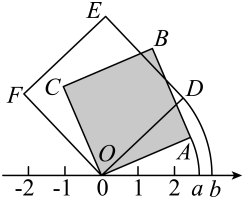 12. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 .
12. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 . 13. 如图,点在反比例函数的图象上,轴于点轴于点 . 一次函数与交于点 , 若为的中点,则的值为 .
13. 如图,点在反比例函数的图象上,轴于点轴于点 . 一次函数与交于点 , 若为的中点,则的值为 . 14. 如图,正方形ABCD的边长为2,对角线AC,BD相交于点 , 以点为圆心,对角线BD的长为半径画弧,交BC的延长线于点 , 则图中阴影部分的面积为.
14. 如图,正方形ABCD的边长为2,对角线AC,BD相交于点 , 以点为圆心,对角线BD的长为半径画弧,交BC的延长线于点 , 则图中阴影部分的面积为. 15. 如图,在平面直角坐标系中,直线l:与x轴交于点 , 以为边作正方形点在y轴上,延长交直线l于点 , 以为边作正方形 , 点在y轴上,以同样的方式依次作正方形 , …,正方形 , 则点的横坐标是 .
15. 如图,在平面直角坐标系中,直线l:与x轴交于点 , 以为边作正方形点在y轴上,延长交直线l于点 , 以为边作正方形 , 点在y轴上,以同样的方式依次作正方形 , …,正方形 , 则点的横坐标是 .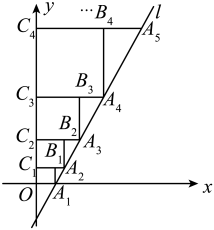 16. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .17. 如图,AC,AD,CE是正五边形ABCDE的对角线,AD与CE相交于点.下列结论:
16. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .17. 如图,AC,AD,CE是正五边形ABCDE的对角线,AD与CE相交于点.下列结论:
①CF平分;②;③四边形ABCF是菱形;④
其中正确的结论是.(填写所有正确结论的序号)三、解答题
-
18. 如图,某育苗基地为了能够最大限度地遮挡夏季炎热的阳光和充分利用冬天的光照,计划在苗圃正上方搭建一个平行于地面的遮阳蓬.已知苗圃的(南北)宽米,该地区一年中正午时刻太阳光与地平面的最大夹角是 , 最小夹角是 . 求遮阳蓬的宽和到地面的距离 .
参考数据: , , , , , .
 19. 某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:
19. 某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:填写人:王朵 综合实践活动报告 时间:2023年4月20日
活动任务:测量古树高度
活动过程
【步骤一】设计测量方案
小组成员讨论后,画出如图①的测量草图,确定需测的几何量.

【步骤二】准备测量工具
自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角,如图②所示准备皮尺.

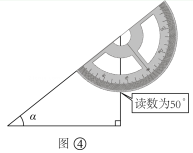
【步骤三】实地测量并记录数据如图③,王朵同学站在离古树一定距离的地方,将这个仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达古树的最高点.
如图④,利用测角仪,测量后计算得出仰角 .
测出眼睛到地面的距离 .
测出所站地方到古树底部的距离 .

 .
..
.
【步骤四】计算古树高度 . (结果精确到)
(参考数据:)
请结合图①、图④和相关数据写出的度数并完成【步骤四】.
四、作图题
-
20. 已知正六边形 , 请仅用无刻度的直尺完成下列作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
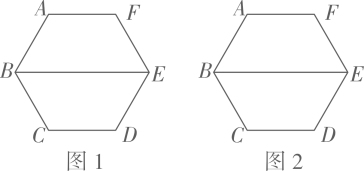 (1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .
(1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .五、综合题
-
21.
 (1)、【操作发现】如图①,剪两张对边平行的纸条,随意交叉叠放在一起,使重合的部分构成一个四边形 . 转动其中一张纸条,发现四边形总是平行四边形其中判定的依据是 .(2)、【探究提升】取两张短边长度相等的平行四边形纸条和( , ),其中 , , 将它们按图②放置,落在边上,与边分别交于点M,N.求证:是菱形.(3)、【结论应用】保持图②中的平行四边形纸条不动,将平行四边形纸条沿或平移,且始终在边上.当时,延长交于点P,得到图③.若四边形的周长为40,(为锐角),则四边形的面积为 .22. 如图,在菱形ABCD中,于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF.
(1)、【操作发现】如图①,剪两张对边平行的纸条,随意交叉叠放在一起,使重合的部分构成一个四边形 . 转动其中一张纸条,发现四边形总是平行四边形其中判定的依据是 .(2)、【探究提升】取两张短边长度相等的平行四边形纸条和( , ),其中 , , 将它们按图②放置,落在边上,与边分别交于点M,N.求证:是菱形.(3)、【结论应用】保持图②中的平行四边形纸条不动,将平行四边形纸条沿或平移,且始终在边上.当时,延长交于点P,得到图③.若四边形的周长为40,(为锐角),则四边形的面积为 .22. 如图,在菱形ABCD中,于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF. (1)、求证:①CD是⊙O的切线;②△DEF∽△DBA;(2)、 若AB=5,DB=6 ,求 .23. 过正方形的顶点作直线 , 点关于直线的对称点为点 , 连接 , 直线交直线于点 .
(1)、求证:①CD是⊙O的切线;②△DEF∽△DBA;(2)、 若AB=5,DB=6 ,求 .23. 过正方形的顶点作直线 , 点关于直线的对称点为点 , 连接 , 直线交直线于点 . (1)、如图1,若 , 则°;(2)、如图1,请探究线段 , , 之间的数量关系,并证明你的结论;(3)、在绕点转动的过程中,设 , 请直接用含的式子表示的长.24. 如图,的对角线交于点 , 分别以点为圆心,长为半径画弧,两弧交于点 , 连接 .
(1)、如图1,若 , 则°;(2)、如图1,请探究线段 , , 之间的数量关系,并证明你的结论;(3)、在绕点转动的过程中,设 , 请直接用含的式子表示的长.24. 如图,的对角线交于点 , 分别以点为圆心,长为半径画弧,两弧交于点 , 连接 . (1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?25.(1)、如图,在矩形中,为边上一点,连接 ,
(1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?25.(1)、如图,在矩形中,为边上一点,连接 ,①若 , 过作交于点 , 求证:;
②若时,则 .
 (2)、如图,在菱形中, , 过作交的延长线于点 , 过作交于点 , 若时,求的值.
(2)、如图,在菱形中, , 过作交的延长线于点 , 过作交于点 , 若时,求的值. (3)、如图,在平行四边形中, , , , 点在上,且 , 点为上一点,连接 , 过作交平行四边形的边于点 , 若时,请直接写出的长.
(3)、如图,在平行四边形中, , , , 点在上,且 , 点为上一点,连接 , 过作交平行四边形的边于点 , 若时,请直接写出的长.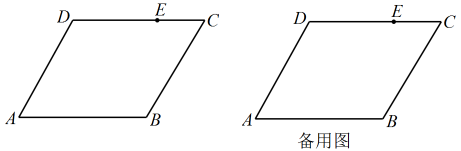 26. 如图,一次函数的图像与反比例函数的图像相交于 , 两点.
26. 如图,一次函数的图像与反比例函数的图像相交于 , 两点. (1)、求反比例函数和一次函数的表达式;(2)、点在x轴负半轴上,连接AP,过点B作 , 交的图像于点Q,连接PQ.当时,若四边形APQB的面积为36,求n的值.27. 阅读与思考:下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.
(1)、求反比例函数和一次函数的表达式;(2)、点在x轴负半轴上,连接AP,过点B作 , 交的图像于点Q,连接PQ.当时,若四边形APQB的面积为36,求n的值.27. 阅读与思考:下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.瓦里尼翁平行四边形
我们知道,如图1,在四边形中,点分别是边 , 的中点,顺次连接 , 得到的四边形是平行四边形.
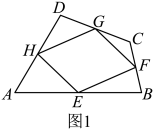
我查阅了许多资料,得知这个平行四边形被称为瓦里尼翁平行四边形.瓦里尼翁是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.

①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.此结论可借助图1证明如下:
证明:如图2,连接 , 分别交于点 , 过点作于点 , 交于点 .
∵分别为的中点,∴ . (依据1)
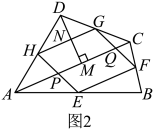
∴ . ∵ , ∴ .
∵四边形是瓦里尼翁平行四边形,∴ , 即 .
∵ , 即 ,
∴四边形是平行四边形.(依据2)∴ .
∵ , ∴ . 同理,…
任务:
(1)、填空:材料中的依据1是指: .依据2是指: .
(2)、请用刻度尺、三角板等工具,画一个四边形及它的瓦里尼翁平行四边形 , 使得四边形为矩形;(要求同时画出四边形的对角线)(3)、在图1中,分别连接得到图3,请猜想瓦里尼翁平行四边形的周长与对角线长度的关系,并证明你的结论.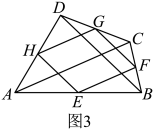
-