2023年中考数学真题分类汇编(全国版):三角形(10)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 , , 的计算公式: , , , 其中 , , 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )A、3,4,5 B、5,12,13 C、6,8,10 D、7,24,252. 第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角 , 算出这个正多边形的边数是( )
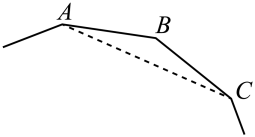 A、9 B、10 C、11 D、123. 如图,是的切线,为切点,连接 . 若 , , , 则的长度是( )
A、9 B、10 C、11 D、123. 如图,是的切线,为切点,连接 . 若 , , , 则的长度是( )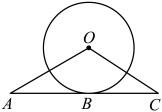 A、 B、 C、 D、4. 如图,在正方形中,点 , 分别在 , 上,连接 , , , . 若 , 则一定等于( )
A、 B、 C、 D、4. 如图,在正方形中,点 , 分别在 , 上,连接 , , , . 若 , 则一定等于( ) A、 B、 C、 D、5. 如图,为的直径,直线与相切于点C,连接 , 若 , 则的度数为( )
A、 B、 C、 D、5. 如图,为的直径,直线与相切于点C,连接 , 若 , 则的度数为( )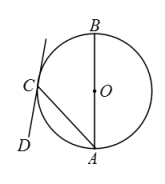 A、 B、 C、 D、6. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( )
A、 B、 C、 D、6. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( ) A、 B、 C、2 D、17. 如图,在正方形中,O为对角线的中点,E为正方形内一点,连接 , , 连接并延长,与的平分线交于点F,连接 , 若 , 则的长度为( )
A、 B、 C、2 D、17. 如图,在正方形中,O为对角线的中点,E为正方形内一点,连接 , , 连接并延长,与的平分线交于点F,连接 , 若 , 则的长度为( )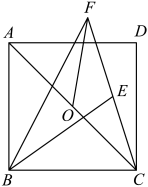 A、2 B、 C、1 D、
A、2 B、 C、1 D、二、填空题
-
8. 在 Rt △ABC中, ∠ACB=90°,AC=6,BC=8,D是AB的中点,则 .9. 如图,边长为2的等边的两个顶点分别在两条射线上滑动,若 , 则的最大值是 .
 10. 如图,在正五边形ABCDE中,连接AC,则∠BAC的度数为 .
10. 如图,在正五边形ABCDE中,连接AC,则∠BAC的度数为 . 11. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .
11. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .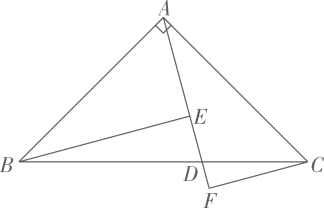 12. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留)
12. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留) 13. 如图,在矩形中, , , E为的中点,连接 , 以E为圆心,长为半径画弧,分别与交于点M,N,则图中阴影部分的面积为 . (结果保留)
13. 如图,在矩形中, , , E为的中点,连接 , 以E为圆心,长为半径画弧,分别与交于点M,N,则图中阴影部分的面积为 . (结果保留)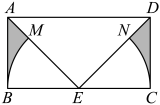 14. 如图,在中, , 是边的中线,若 , , 则的长度为 .
14. 如图,在中, , 是边的中线,若 , , 则的长度为 .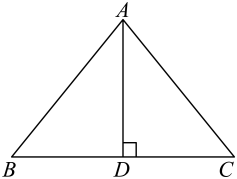 15. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。
15. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。 16. 如图,在纸片中, , 是边上的中线,将沿折叠,当点落在点处时,恰好 , 若 , 则 .
16. 如图,在纸片中, , 是边上的中线,将沿折叠,当点落在点处时,恰好 , 若 , 则 .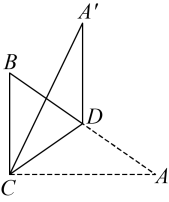 17. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .
17. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .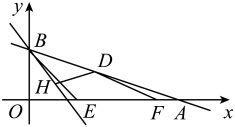
三、解答题
-
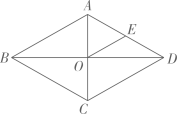
18. 如图,菱形的对角线相交于点为的中点, , .求的长及的值.
四、作图题
-
19. 学习了平行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:
用直尺和圆规,作的垂直平分线交于点E,交于点F,垂足为点O.(只保留作图痕迹)
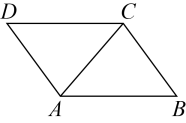
已知:如图,四边形是平行四边形,是对角线,垂直平分 , 垂足为点O.
求证: .
证明:∵四边形是平行四边形,
∴ .
∴ ▲ .
∵垂直平分 ,
∴ ▲ .
又 ▲ .
∴ .
∴ .
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ▲ .
五、综合题
-
20. 如图1,一大一小两个等腰直角三角形叠放在一起, , 分别是斜边 , 的中点, .
 (1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.21. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.
(1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.21. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.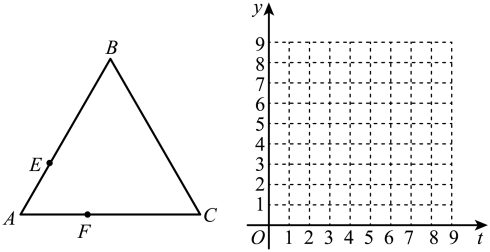 (1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.22. 为了满足市民的需求,我市在一条小河两侧开辟了两条长跑锻炼线路,如图;①;② . 经勘测,点B在点A的正东方,点C在点B的正北方千米处,点D在点C的正西方千米处,点D在点A的北偏东方向,点E在点A的正南方,点E在点B的南偏西方向.(参考数据:
(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.22. 为了满足市民的需求,我市在一条小河两侧开辟了两条长跑锻炼线路,如图;①;② . 经勘测,点B在点A的正东方,点C在点B的正北方千米处,点D在点C的正西方千米处,点D在点A的北偏东方向,点E在点A的正南方,点E在点B的南偏西方向.(参考数据: (1)、求AD的长度.(结果精确到1千米)(2)、由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?23. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.
(1)、求AD的长度.(结果精确到1千米)(2)、由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?23. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y. (1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.24. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.24. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.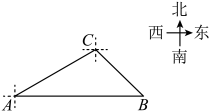 (1)、求B养殖场与灯塔C的距离(结果精确到个位);(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据: , )25. 如图1,在中,是边上不与重合的一个定点.于点 , 交于点 . 是由线段绕点顺时针旋转得到的,的延长线相交于点 .
(1)、求B养殖场与灯塔C的距离(结果精确到个位);(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据: , )25. 如图1,在中,是边上不与重合的一个定点.于点 , 交于点 . 是由线段绕点顺时针旋转得到的,的延长线相交于点 .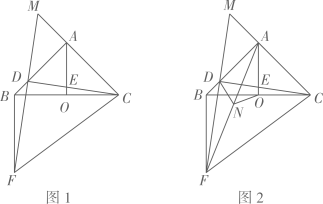 (1)、求证:;(2)、求的度数;(3)、若是的中点,如图2.求证: .26. 如图,是的直径, , 的弦于点 , . 过点作的切线交的延长线于点 , 连接 .
(1)、求证:;(2)、求的度数;(3)、若是的中点,如图2.求证: .26. 如图,是的直径, , 的弦于点 , . 过点作的切线交的延长线于点 , 连接 . (1)、求证:平分;(2)、为上一点,连接交于点 , 若 , 求的长.27. 在中, , , 点为线段上一动点,连接 .
(1)、求证:平分;(2)、为上一点,连接交于点 , 若 , 求的长.27. 在中, , , 点为线段上一动点,连接 . (1)、如图1,若 , , 求线段的长.(2)、如图2,以为边在上方作等边 , 点是的中点,连接并延长,交的延长线于点 . 若 , 求证: .(3)、在取得最小值的条件下,以为边在右侧作等边 . 点为所在直线上一点,将沿所在直线翻折至所在平面内得到 . 连接 , 点为的中点,连接 , 当取最大值时,连接 , 将沿所在直线翻折至所在平面内得到 , 请直接写出此时的值.28. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .
(1)、如图1,若 , , 求线段的长.(2)、如图2,以为边在上方作等边 , 点是的中点,连接并延长,交的延长线于点 . 若 , 求证: .(3)、在取得最小值的条件下,以为边在右侧作等边 . 点为所在直线上一点,将沿所在直线翻折至所在平面内得到 . 连接 , 点为的中点,连接 , 当取最大值时,连接 , 将沿所在直线翻折至所在平面内得到 , 请直接写出此时的值.28. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .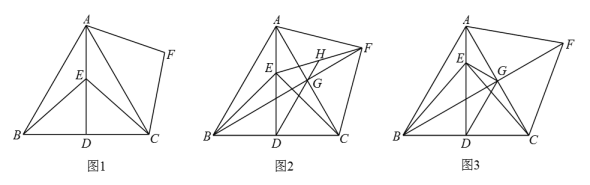 (1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.
(1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.
-
-