2023年中考数学真题分类汇编(全国版):三角形(9)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )A、 B、 C、 D、2. 如图,以钝角三角形ABC最长边BC为边向外作矩形 , 连结 , 设 , , 的面积分别为 , 若要求出的值,只需知道( )
 A、的面积 B、的面积 C、的面积 D、矩形的面积3. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:
A、的面积 B、的面积 C、的面积 D、矩形的面积3. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为( ) A、 B、 C、 D、4. 下列命题中,是真命题的是( )A、平行四边形是轴对称图形 B、对角线互相垂直的四边形是菱形 C、到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D、在中,若 , 则是直角三角形5. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( )
A、 B、 C、 D、4. 下列命题中,是真命题的是( )A、平行四边形是轴对称图形 B、对角线互相垂直的四边形是菱形 C、到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D、在中,若 , 则是直角三角形5. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( ) A、 B、 C、 D、6. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( )
A、 B、 C、 D、6. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( ) A、 B、 C、 D、7. 如图,矩形内接于 , 分别以为直径向外作半圆.若 , 则阴影部分的面积是( )
A、 B、 C、 D、7. 如图,矩形内接于 , 分别以为直径向外作半圆.若 , 则阴影部分的面积是( )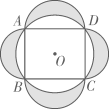 A、 B、 C、 D、208. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( )
A、 B、 C、 D、208. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( ) A、12 B、14 C、18 D、249. 如图,在Rt中, , 以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点.若 , 则的值是( )
A、12 B、14 C、18 D、249. 如图,在Rt中, , 以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点.若 , 则的值是( )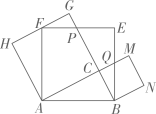 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 如图,已知 , 点B,E,C,F依次在同一条直线上. 若 , , 则CF的长为.
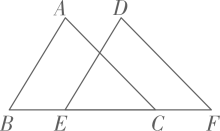 11. 如图,中,为对角线,分别以点A、B为圆心,以大于的长为半径画弧,两弧相交于点M、N,作直线交于点E,交于点F,若 , , , 则的长为 .
11. 如图,中,为对角线,分别以点A、B为圆心,以大于的长为半径画弧,两弧相交于点M、N,作直线交于点E,交于点F,若 , , , 则的长为 . 12. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 .
12. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 . 13. 一个三角形的两边长分别是3和5,则第三边长可以是.(只填一个即可)14. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm.
13. 一个三角形的两边长分别是3和5,则第三边长可以是.(只填一个即可)14. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm. 15. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出. 该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳名观众同时观看演出.(取3.14,取1.73)
15. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出. 该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳名观众同时观看演出.(取3.14,取1.73) 16. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则.
16. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则. 17. 如图,是正方形边的中点,是正方形内一点,连接 , 线段以为中心逆时针旋转得到线段 , 连接 . 若 , , 则的最小值为 .
17. 如图,是正方形边的中点,是正方形内一点,连接 , 线段以为中心逆时针旋转得到线段 , 连接 . 若 , , 则的最小值为 . 18. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。
18. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。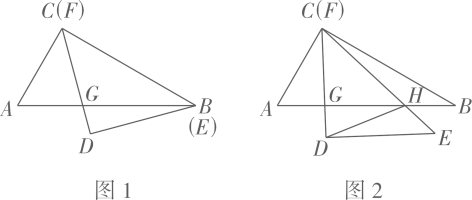 19. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .
19. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .三、解答题
-
20. 【问题背景】
如图1,数学实践课上,学习小组进行探究活动,老师要求大家对矩形进行如下操作:①分别以点为圆心,以大于的长度为半径作弧,两弧相交于点 , , 作直线交于点 , 连接;②将沿翻折,点的对应点落在点处,作射线交于点 .

【问题提出】
在矩形中, , 求线段的长.
【问题解决】
经过小组合作、探究、展示,其中的两个方案如下:
方案一:连接 , 如图2.经过推理、计算可求出线段的长;
方案二:将绕点旋转至处,如图3.经过推理、计算可求出线段的长.
请你任选其中一种方案求线段的长.
四、作图题
-
21. 学习了平行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:
用直尺和圆规,作的垂直平分线交于点E,交于点F,垂足为点O.(只保留作图痕迹)
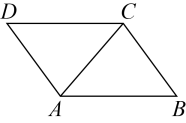
已知:如图,四边形是平行四边形,是对角线,垂直平分 , 垂足为点O.
求证: .
证明:∵四边形是平行四边形,
∴ .
∴ ▲ .
∵垂直平分 ,
∴ ▲ .
又 ▲ .
∴ .
∴ .
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ▲ .
五、综合题
-
22. 如图,点在第一象限内,与轴相切于点 , 与轴相交于点C,D.连结AB,过点作于点.
 (1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.23. 如图,在中, .
(1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.23. 如图,在中, . (1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.24. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上.
(1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.24. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上. (1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.25. 问题:如何设计“倍力桥”的结构?
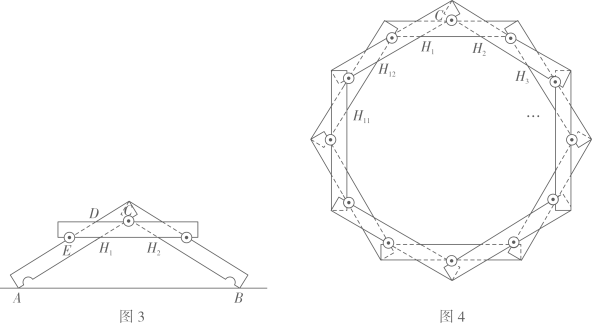
(1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.25. 问题:如何设计“倍力桥”的结构?图1是搭成的“倍力桥”,纵梁a,c夹住横梁 , 使得横梁不能移动,结构稳固.
图2是长为 , 宽为的横梁侧面示意图,三个凹槽都是半径为的半圆.圆心分别为 , 纵梁是底面半径为的圆柱体.用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.


探究1:图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,D,H1 , H2是横梁侧面两边的交点.测得AB=32cm,点C到AB的距离为12cm.试判断四边形CDEH1的形状,并求的值.
探究2:若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.
①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求的值;
②若有n根横梁绕成的环(n为偶数,且n≥6),试用关于n的代数式表示内部形成的多边形的周长.
 26. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
26. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.在中, , , D是AB边上一点,且(n为正整数),E是AC边上的动点,过点D作DE的垂线交直线BC于点F.
 (1)、【初步感知】
(1)、【初步感知】如图1,当时,兴趣小组探究得出结论: , 请写出证明过程.
(2)、【深入探究】①如图2,当 , 且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).
(3)、【拓展运用】如图3,连接EF,设EF的中点为M. 若 , 求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
27. 如图,内接于是延长线上的一点, , 相交于点 .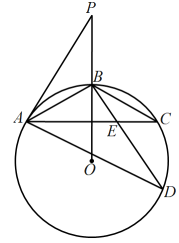 (1)、求证:是的切线;(2)、若 , , 求的长.28. 阅读理解题:
(1)、求证:是的切线;(2)、若 , , 求的长.28. 阅读理解题:阅读材料:
如图1,四边形是矩形,是等腰直角三角形,记为、为 , 若 , 则 .

证明:设 , ∵ , ∴ ,
易证
∴ ,
∴
∴ ,
若时,当 , 则 .
同理:若时,当 , 则 .
根据上述材料,完成下列问题:
如图2,直线与反比例函数的图象交于点 , 与轴交于点 . 将直线绕点顺时针旋转后的直线与轴交于点 , 过点作轴于点 , 过点作轴于点 , 已知 .
 (1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.
(1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.
-
-

