2023年中考数学真题分类汇编(全国版):三角形(8)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
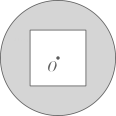 A、 B、2 C、 D、2. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
A、 B、2 C、 D、2. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ). A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( ) A、 B、 C、 D、4. 如图2,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若 , 则( )
A、 B、 C、 D、4. 如图2,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若 , 则( ) A、2 B、 C、3 D、45. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A、2 B、 C、3 D、45. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( ) A、 B、 C、 D、6. 《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、为半径的圆弧,N是的中点, . “会圆术”给出的弧长的近似值计算公式: . 当 , 时,则的值为( )
A、 B、 C、 D、6. 《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、为半径的圆弧,N是的中点, . “会圆术”给出的弧长的近似值计算公式: . 当 , 时,则的值为( ) A、 B、 C、 D、7. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )
A、 B、 C、 D、7. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )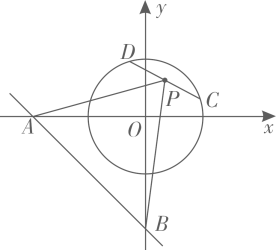 A、8 B、6 C、4 D、38. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( )
A、8 B、6 C、4 D、38. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( ) A、 B、 C、 D、9. 如图,和是以点为直角顶点的等腰直角三角形,把以为中心顺时针旋转,点为射线、的交点.若 , . 以下结论:
A、 B、 C、 D、9. 如图,和是以点为直角顶点的等腰直角三角形,把以为中心顺时针旋转,点为射线、的交点.若 , . 以下结论:①;②;
③当点在的延长线上时,;
④在旋转过程中,当线段最短时,的面积为 .
其中正确结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 如图,中,是中线,分别以点A,点B为圆心,大于长为半径作弧,两孤交于点M,N.直线交于点E.连接交于点F.过点D作 , 交于点G.若 , 则的长为 .
 11. 如图,在菱形中, , 连结 , 以点为圆心,长为半径作弧,交直线于点 , 连结 , 则的度数是.
11. 如图,在菱形中, , 连结 , 以点为圆心,长为半径作弧,交直线于点 , 连结 , 则的度数是.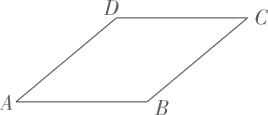 12. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.
12. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.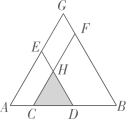 (1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .13. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .
(1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .13. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .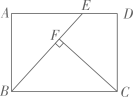 14. 若三角形三个内角的比为1:2:3,则这个三角形按角分类是三角形.15. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
14. 若三角形三个内角的比为1:2:3,则这个三角形按角分类是三角形.15. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号) 16. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为
16. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为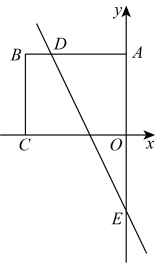 17. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)
17. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)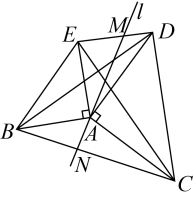
三、作图题
-
18. 如图,在的方格纸ABCD中,每个小方格的边长为1.已知格点 , 请按要求画格点三角形(顶点均在格点上).
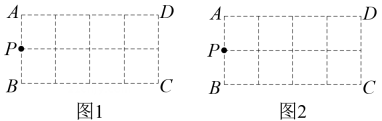 (1)、在图1中画一个等腰三角形PEF,使底边长为 , 点在BC上,点在AD上,再画出该三角形绕矩形ABCD的中心旋转后的图形.(2)、在图2中画一个Rt , 使 , 点在上,点在AD上,再画出该三角形向右平移1个単位后的图形.
(1)、在图1中画一个等腰三角形PEF,使底边长为 , 点在BC上,点在AD上,再画出该三角形绕矩形ABCD的中心旋转后的图形.(2)、在图2中画一个Rt , 使 , 点在上,点在AD上,再画出该三角形向右平移1个単位后的图形.四、综合题
-
19. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.
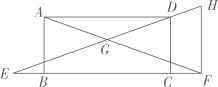 (1)、求证:.(2)、当时,求EF的长.20. 如图,四边形ABCD中, , , BD为对角线.
(1)、求证:.(2)、当时,求EF的长.20. 如图,四边形ABCD中, , , BD为对角线. (1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).21. 如图9,在中, , 点D为AB边上任意一点(不与点A、B重合),过点D作 , , 分别交AC、BC于点E、F,连结EF.
(1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).21. 如图9,在中, , 点D为AB边上任意一点(不与点A、B重合),过点D作 , , 分别交AC、BC于点E、F,连结EF. (1)、求证:四边形ECFD是矩形;(2)、若 , 求点C到EF的距离.22. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 .
(1)、求证:四边形ECFD是矩形;(2)、若 , 求点C到EF的距离.22. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 . (1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.23. 如图,已知是的外接圆, , D是圆上一点,E是DC延长线上一点,连结AD,AE,且 .
(1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.23. 如图,已知是的外接圆, , D是圆上一点,E是DC延长线上一点,连结AD,AE,且 . (1)、求证:直线AE是是的切线;(2)、若 , 的半径为3,求AD的长.24. 如图,在菱形ABCD中,于点E,于点F,连结EF。
(1)、求证:直线AE是是的切线;(2)、若 , 的半径为3,求AD的长.24. 如图,在菱形ABCD中,于点E,于点F,连结EF。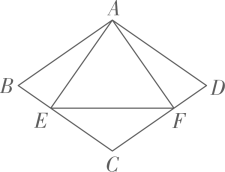 (1)、求证:;(2)、若 , 求的度数。25. 在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动
(1)、求证:;(2)、若 , 求的度数。25. 在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动【问题情境】
刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容:
如图,将一个三角形纸板绕点A逆时针旋转到达的位置,那么可以得到:
;( )

刘老师进一步谈到:图形的旋转蕴含于自然界的运动变化规律中,即“变”中蕴含着“不变”,这是我们解决图形旋转的关键故数学就是一门哲学.
(1)、【问题解决】
上述问题情境中“( )”处应填理由:;(2)、如图,小王将一个半径为 , 圆心角为的扇形纸板ABC绕点O逆时针旋转到达扇形纸板的位置.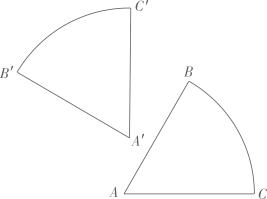
①请在图中作出点O;
②如果 , 则在旋转过程中,点B经过的路径长为;
(3)、【问题拓展】小李突发奇想,将与(2)中完全相同的两个扇形纸板重叠,一个固定在墙上,使得一边位于水平位置另一个在孤的中点处固定,然后放开纸板,使其摆动到竖直位置时静止此时,两个纸板重叠部分的面积是多少呢?如图所示,请你帮助小李解决这个问题.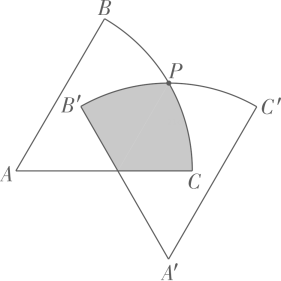 26. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 .
26. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 . (1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.27. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且).
(1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.27. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .
-