2023年中考数学真题分类汇编(全国版):三角形(7)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
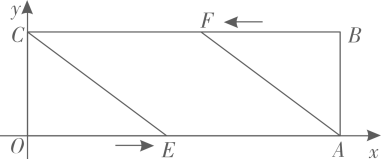
1. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
 A、 B、 C、 D、2. 如图,在中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线分别与边相交于点D,E,连接 . 若 , 则的长为( )
A、 B、 C、 D、2. 如图,在中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线分别与边相交于点D,E,连接 . 若 , 则的长为( ) A、9 B、8 C、7 D、63. 下列说法正确的是( )A、三角形的一个外角等于两个内角的和 B、对角线相等且互相垂直的四边形是正方形 C、在一组数据11,9,7,8,6,8,12,8中,众数和中位数都是8 D、甲乙两组各10名同学参加“安全知识竞赛”,若两组同学的平均成绩相同,甲组的方差 , 乙组的方差 , 则甲组同学的成绩比乙组同学的成绩稳定4. 如图,在等腰直角中, , 以点为圆心,为半径画弧,交于点 , 以点为圆心,为半径画弧,交于点 , 则图中阴影部分的面积是( )
A、9 B、8 C、7 D、63. 下列说法正确的是( )A、三角形的一个外角等于两个内角的和 B、对角线相等且互相垂直的四边形是正方形 C、在一组数据11,9,7,8,6,8,12,8中,众数和中位数都是8 D、甲乙两组各10名同学参加“安全知识竞赛”,若两组同学的平均成绩相同,甲组的方差 , 乙组的方差 , 则甲组同学的成绩比乙组同学的成绩稳定4. 如图,在等腰直角中, , 以点为圆心,为半径画弧,交于点 , 以点为圆心,为半径画弧,交于点 , 则图中阴影部分的面积是( ) A、 B、 C、 D、5. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )
A、 B、 C、 D、5. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )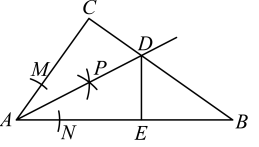 A、 B、 C、 D、6. 如图,中, , 则的度数为( )
A、 B、 C、 D、6. 如图,中, , 则的度数为( ) A、 B、 C、 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )
A、 B、 C、 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )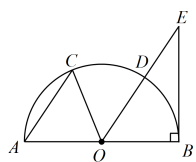 A、 B、 C、 D、8. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、 B、 C、 D、8. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )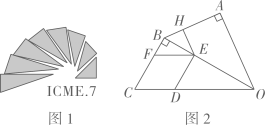 A、 B、 C、 D、9. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )
A、 B、 C、 D、9. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )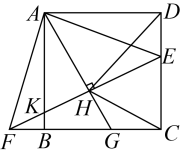 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 如图,在中,若 , , , 则 .
 11. 如图,在中, . 以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 .
11. 如图,在中, . 以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 . 12. 如图,菱形中, , , , 垂足分别为 , , 若 , 则 .
12. 如图,菱形中, , , , 垂足分别为 , , 若 , 则 .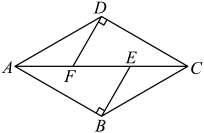 13. 如图, . 过点作 , 延长到 , 使 , 连接 . 若 , 则 . (结果保留根号)
13. 如图, . 过点作 , 延长到 , 使 , 连接 . 若 , 则 . (结果保留根号)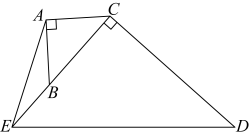 14. 如图,在边长为3的正方形的外侧,作等腰三角形 , .
14. 如图,在边长为3的正方形的外侧,作等腰三角形 , .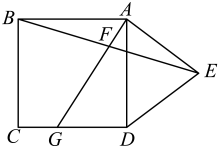 (1)、的面积为;(2)、若F为的中点,连接并延长,与相交于点G,则的长为 .15. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若 , 则每个直角三角形的面积为 .
(1)、的面积为;(2)、若F为的中点,连接并延长,与相交于点G,则的长为 .15. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若 , 则每个直角三角形的面积为 .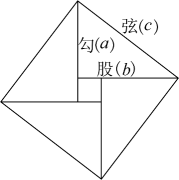 16. 如图,中, , 以点B为圆心,适当长为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点E,作射线交于点D,则线段的长为 .
16. 如图,中, , 以点B为圆心,适当长为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点E,作射线交于点D,则线段的长为 . 17. 如图,已知正方形的边长为1,点E、F分别在边上,将正方形沿着翻折,点B恰好落在边上的点处,如果四边形与四边形的面积比为3∶5,那么线段的长为 .
17. 如图,已知正方形的边长为1,点E、F分别在边上,将正方形沿着翻折,点B恰好落在边上的点处,如果四边形与四边形的面积比为3∶5,那么线段的长为 .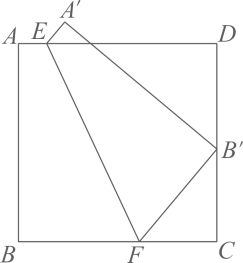
三、解答题
-
18. 如图, .
求证: .
四、作图题
-
19. 如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
 (1)、线段的长为;(2)、若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .
(1)、线段的长为;(2)、若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .五、综合题
-
20. 如图,一次函数的图象与轴交于点 , 与反比例函数的图象交于点 .
 (1)、求点的坐标;(2)、用的代数式表示;(3)、当的面积为9时,求一次函数的表达式.21. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .
(1)、求点的坐标;(2)、用的代数式表示;(3)、当的面积为9时,求一次函数的表达式.21. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .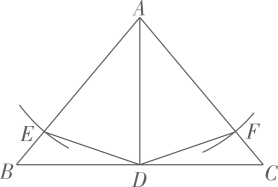 (1)、求证:;(2)、若 , 求的度数.22. 如图,在中, , 点D是上一点,且 , 点O在上,以点O为圆心的圆经过C、D两点.
(1)、求证:;(2)、若 , 求的度数.22. 如图,在中, , 点D是上一点,且 , 点O在上,以点O为圆心的圆经过C、D两点.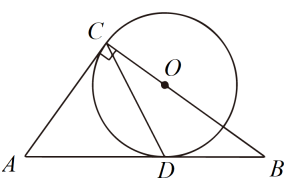 (1)、试判断直线与的位置关系,并说明理由;(2)、若的半径为3,求的长.23. 如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点 , 与轴交于点 .
(1)、试判断直线与的位置关系,并说明理由;(2)、若的半径为3,求的长.23. 如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点 , 与轴交于点 .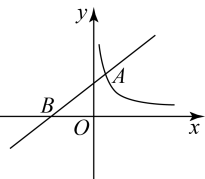 (1)、求一次函数和反比例函数的解析式.(2)、点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.24. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D.
(1)、求一次函数和反比例函数的解析式.(2)、点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.24. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D. (1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.25. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .
(1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.25. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .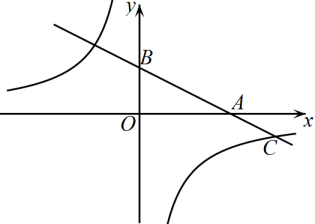 (1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.26.
(1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.26.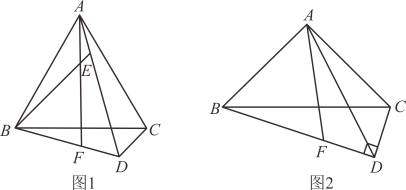 (1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.
(1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.①求证:;
②用等式写出线段 , , 的数量关系,并说明理由.
(2)、【模型应用】如图2,是直角三角形, , , 垂足为 , 点关于的对称点在边上.用等式写出线段 , , 的数量关系,并说明理由.
(3)、【模型迁移】在(2)的条件下,若 , , 求的值.
27. 【问题情境】在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动,两块三角板分别记作和 , 设 .
【操作探究】
如图1,先将和的边、重合,再将绕着点A按顺时针方向旋转,旋转角为 , 旋转过程中保持不动,连接 .
 (1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .28. 如图,正方形中,点在边上,点是的中点,连接 , .
(1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .28. 如图,正方形中,点在边上,点是的中点,连接 , . (1)、求证:;(2)、将绕点逆时针旋转,使点的对应点落在上,连接 . 当点在边上运动时(点不与 , 重合),判断的形状,并说明理由.(3)、在(2)的条件下,已知 , 当时,求的长.
(1)、求证:;(2)、将绕点逆时针旋转,使点的对应点落在上,连接 . 当点在边上运动时(点不与 , 重合),判断的形状,并说明理由.(3)、在(2)的条件下,已知 , 当时,求的长.
-
-