2023年中考真题分类汇编(全国版):三角形(6)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 下列长度的各组线段能组成一个三角形的是( )A、 B、 C、 D、2. 如图1,在中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中长与运动时间t(单位:s)的关系如图2,则的长为( )
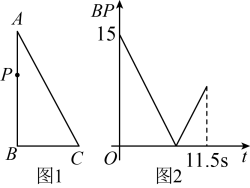 A、 B、 C、17 D、3. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( )
A、 B、 C、17 D、3. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( ) A、5 B、4 C、3 D、24. 如图,在中,以点为圆心,适当长为半径作弧,交于点 , 交于点 , 分别以点 , 为圆心,大于长为半径作弧,两弧在的内部交于点 , 作射线交于点 . 若 , , 则的长为( )
A、5 B、4 C、3 D、24. 如图,在中,以点为圆心,适当长为半径作弧,交于点 , 交于点 , 分别以点 , 为圆心,大于长为半径作弧,两弧在的内部交于点 , 作射线交于点 . 若 , , 则的长为( ) A、 B、1 C、 D、25. 如图,在中,弦相交于点P,若 , 则的度数为( )
A、 B、1 C、 D、25. 如图,在中,弦相交于点P,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,在中, , 以点A为圆心,以的长为半径作弧交于点D,连接 , 再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线交于点E,连接 , 则下列结论中不正确的是( )
A、 B、 C、 D、6. 如图,在中, , 以点A为圆心,以的长为半径作弧交于点D,连接 , 再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线交于点E,连接 , 则下列结论中不正确的是( ) A、 B、 C、 D、7. 下列说法错误的是( )A、成语“水中捞月”表示的事件是不可能事件 B、一元二次方程有两个相等的实数根 C、任意多边形的外角和等于 D、三角形三条中线的交点叫作三角形的重心8. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( )
A、 B、 C、 D、7. 下列说法错误的是( )A、成语“水中捞月”表示的事件是不可能事件 B、一元二次方程有两个相等的实数根 C、任意多边形的外角和等于 D、三角形三条中线的交点叫作三角形的重心8. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( ) A、 B、 C、 D、9. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( )
A、 B、 C、 D、9. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( ) A、2 B、4 C、5 D、6
A、2 B、4 C、5 D、6二、填空题
-
10. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 .
 11. 在中,的对边分别为a、b、c,且满足 , 则的值为 .12. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中, , , 对角线与交于点O,点E为边上的一个动点, , , 垂足分别为点F,G,则 .
11. 在中,的对边分别为a、b、c,且满足 , 则的值为 .12. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中, , , 对角线与交于点O,点E为边上的一个动点, , , 垂足分别为点F,G,则 . 13. 如图,在菱形中, , 则的长为 .
13. 如图,在菱形中, , 则的长为 .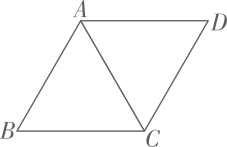 14. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .
14. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .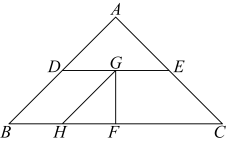 15. 如图,在中, , D为上一点,若是的角平分线,则 .
15. 如图,在中, , D为上一点,若是的角平分线,则 . 16. 如图,在矩形中, , M是边上一动点(不含端点),将沿直线对折,得到 . 当射线交线段于点P时,连接 , 则的面积为;的最大值为 .
16. 如图,在矩形中, , M是边上一动点(不含端点),将沿直线对折,得到 . 当射线交线段于点P时,连接 , 则的面积为;的最大值为 . 17. 如图,平分等边的面积,折叠得到分别与相交于两点.若 , 用含的式子表示的长是 .
17. 如图,平分等边的面积,折叠得到分别与相交于两点.若 , 用含的式子表示的长是 . 18. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 .
18. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 . 19. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
19. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
三、解答题
-
20. 如图,BD是等边△ABC的中线,以D为圆心,DB的长为半径画弧,交BC的延长线于E,连接DE.求证:CD=CE.

四、作图题
-
21. 如图,在方格纸中按要求画图,并完成填空.
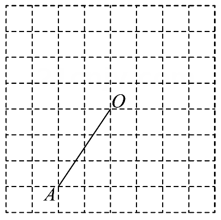
⑴画出线段绕点O顺时针旋转后得到的线段 , 连接;
⑵画出与关于直线对称的图形,点A的对称点是C;
⑶填空:的度数为 ▲ .
五、综合题
-
22. 如图,都是的半径, .
 (1)、求证:;(2)、若 , 求的半径.23. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 .
(1)、求证:;(2)、若 , 求的半径.23. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 . (1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.24. 如图,和相交于点 , , . 点、分别是、的中点.
(1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.24. 如图,和相交于点 , , . 点、分别是、的中点. (1)、求证:;(2)、当时,求证:四边形是矩形.25. 如图,是的直径,是一条弦,D是的中点,于点E,交于点F,交于点H,交于点G.
(1)、求证:;(2)、当时,求证:四边形是矩形.25. 如图,是的直径,是一条弦,D是的中点,于点E,交于点F,交于点H,交于点G.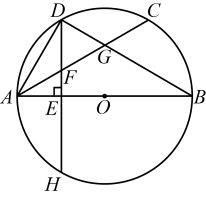 (1)、求证: .(2)、若 , 求的半径.26. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , .
(1)、求证: .(2)、若 , 求的半径.26. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , .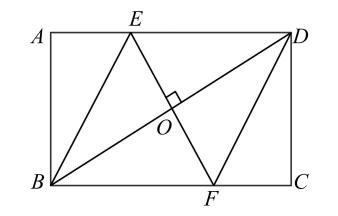 (1)、证明:;(2)、连接、 , 证明:四边形是菱形.27. 如图,内接于 , 是的直径,是上的一点,平分 , , 垂足为 , 与相交于点 .
(1)、证明:;(2)、连接、 , 证明:四边形是菱形.27. 如图,内接于 , 是的直径,是上的一点,平分 , , 垂足为 , 与相交于点 . (1)、求证:是的切线;(2)、当的半径为 , 时,求的长.28. 1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.(1)、下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
(1)、求证:是的切线;(2)、当的半径为 , 时,求的长.28. 1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.(1)、下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)当的三个内角均小于时,
如图1,将绕,点C顺时针旋转得到 , 连接 ,
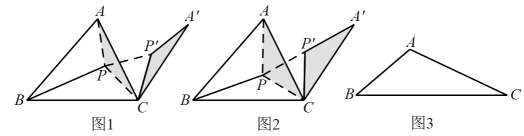
由 , 可知为三角形,故 , 又 , 故 ,
由可知,当B,P, , A在同一条直线上时,取最小值,如图2,最小值为 , 此时的P点为该三角形的“费马点”,且有;
已知当有一个内角大于或等于时,“费马点”为该三角形的某个顶点.如图3,若 , 则该三角形的“费马点”为点.
(2)、如图4,在中,三个内角均小于 , 且 , 已知点P为的“费马点”,求的值; (3)、如图5,设村庄A,B,C的连线构成一个三角形,且已知 . 现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/ , a元/ , 元/ , 选取合适的P的位置,可以使总的铺设成本最低为元.(结果用含a的式子表示)
(3)、如图5,设村庄A,B,C的连线构成一个三角形,且已知 . 现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/ , a元/ , 元/ , 选取合适的P的位置,可以使总的铺设成本最低为元.(结果用含a的式子表示)
-
-

